Inscription / Connexion Nouveau Sujet
Section d'un polygone par un plan
Bonsoir, j'ai un tour petit truc à clarifier avant mon devoir de demain, vous pouvez m'aider svp
Je vous montre d'abord l'exo en question
Exercice
Soit un tétraèdre ABCD et un plan (EFG) tel
que :
E centre de gravité du triangle ABD,
vectBF=vectBC
*** il est interdit de bidouiller les symboles de l'ile : ça ne marche pas
les seuls symboles existants sont ceux de la barre d'outils, non modifiables ***
vectCG=vectCA *** idem ***
Comme dans le schéma la section du tétraèdre par le plan EFG est le quadrilatère SGFQ
Mais ma question est:
Si on regarde (
F) on voit qu'elle coupe à un moment donné la droite AB (appelons ce point par exemple P), peut-on dire aussi que la section du tétraèdre par le plan CGE est le quadrilatère SGFP
A peu près la même chose pour le suivant
*** un seul exo par sujet ***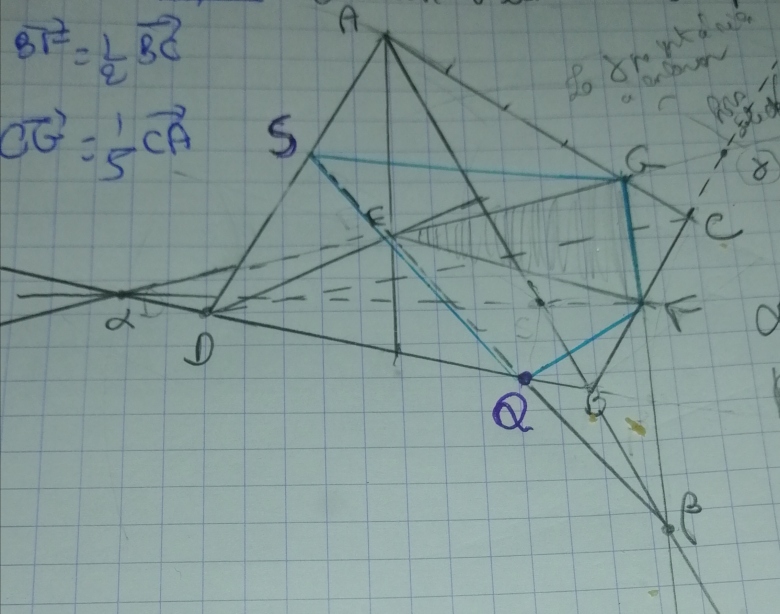
** image supprimée **
** image en double supprimée **
*** citation inutile supprimée
** image supprimée ** la correction de cette image de l'exo 2 est supprimée avec l'exo 2
Bonjour,
ta première figure est complètement incompréhensible en l'absence d'explications sur ce qui est construit dans quel; ordre et pourquoi
la seconde est en double, j'efface une des deux copies identiques.
et de toute façon idem : manque les explications.
de toute façon la section d'un polyèdre convexe par un plan est forcément un et un seul polygone convexe.
ni qu'il y avait en vrai plusieurs exos différents dans la même discussion rendant tout ça complètement incompréhensible
un exo = une et une seule discussion
moi je jette l'éponge devant un tel fatras
je répète ce que j'ai dit :
de toute façon la section d'un polyèdre convexe par un plan est forcément un et un seul polygone convexe.
et si tu penses le contraire ou que ce n'est pas celui du corrigé, c'est très certainement que tes prétendues intersections de droites dans l'espace n'existent pas
que ce sont uniquement des illusions de la perspective
(et pas envie de creuser d'avantage le fatras)
j'ai fait un peu de ménage là dedans
je refais une figure du tétraèdre et rien que du tétraèdre (le pavé est un autre exo et on n'en discutera pas du tout ici dans cette discussion point barre)
Désolé un exo par poste, je m'en excuse
Donc du coup considérons le cas du tétraèdre
Explixation
Dans le plan (ABD)
(EG) et (DB) se coupent en (( appartient à (EGF))
(AB) et (GF) se coupent en 
(( appartient à EGF)
(E) coupe (BD) en Q (Q appartient à EFG)
(E) coupe (AD) en S (S appartient à EFG)
Donc, la section du pavé droit par le plan (EFG) est le quadrilatère SGFQ
NB
, sont des points tracé hors solide
J'espère que maintenant c'est un peu plus clair
Si vous regardez sur mon schéma (F) coupe (AB) en un point(je l'appelle T)
Pourquoi est il faux de considérer ce point qui est sur la figure pourtant
Moi je voulais dire que le quadrilatère c' est SGFT
la construction correcte est :
la droite (GF) fait partie du plan (ABC) elle coupe (AB) en β
ce point appartient aussi au plan (ABD)
la droite (βE) appartient à ce plan (ABD) et coupe (AD) en P et (BD) en Q
on complète le quadrilatère FGPQ
S ne fait pas partie de ce plan (EFG) (c'est juste pour "matérialiser" que E est sur la médiane [BS] )
tu ne dis pas du tout comment serait construit ton point α
de toute façon (αF) est dans le plan (BCD) et ne risque pas de couper (AB) dont le seul point commun avec ce plan est le point D !
comme je disait (αF) coupe (AB) de façon illusoire (perspective) car ces deux droites ne sont même pas dans un même plan !
EG et DB se coupent en
certainement pas !! ces deux droites ne sont même pas dans un même plan et ne risquent pas de se couper
là encore c'est de l'illusion due à la perspective.
Merci beaucoup j'ai enfin compris mon erreur.
Leçon àtirer
Il faut que deux droites soient dans le même plan pour qu'i' ait intersection en un vrai point non fictif(perspective)
C'est ça, n'est-ce pas ?
Annuler
connectez vous