bonjour,

et c'est quoi ce "théorème d'incidence" ???

Soient deux plans parallèles P et Q.
Si un plan R est parallèle à l'un, alors il est parallèle à l'autre et les droites d'intersection sont parallèles.

Le problème, c'est que j'ai déjà utilisé le théorème d'incidence pour la première méthode, donc je ne peux plus utiliser le parallélisme.

la droite d'intersection de deux plans parallèles ??? ...

Soient deux plans parallèles P et Q.
Si un plan R est parallèle sécant à l'un, alors il est parallèle sécant à l'autre et les droites d'intersection sont parallèles.

parce que :
Si un plan R est parallèle à l'un, alors il est parallèle à l'autre est vrai
mais il n'y a alors aucune droite d'intersection !!

faut pas tout mélanger !!

effectivement on peut utiliser ce théorème pour construire directement la section sur la face ADHE, vu qu'on connait celle sur BCGF

sans utiliser ce théorème, par exemple que penses tu de la droite (KN) ? et de son intersection avec le plan (ADHE) ?


nota un peu hors sujet, quoique ... :
en fait c'est une arnaque car le théorème d'incidence a déja été utilisé pour affirmer que IL est parallèle à JB ...
il veulent dire peut être sans utiliser une nouvelle fois ce théorème.

comprenons ce que veut dire réellement la construction de IL etc ci-dessus
et considérons la même construction avec un hexaèdre quelconque (pas cubique pour un sou) :



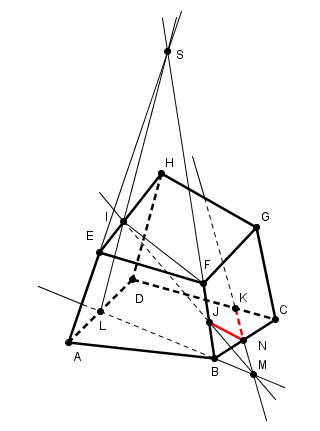
(et tant qu'à faire les milieux ça ne veut rien dire non plus, j'ai mis I, J, K n'importe où sur les arêtes)

(AE) et (BF) se coupent en un point S
la droite (SI) appartient donc au plan (BIJ) ce qui permet de construire l'intersection L de ce plan avec (AD) puis M de (IJ) avec le plan (ABCD) etc
évidemment le point S n'existant pas pour un cube, cette construction ne marche pas et est remplacée par le théorème d'incidence pour affirmer que (IL) est parallèle à (BF)

ça donne peut être toutefois une idée pour s'en sortir ... c'est à dire ne pas utiliser DU TOUT le théorème d'incidence :
utiliser une autre droite que (BF), qui contiendrait aussi le point J mais qui couperait (AE) ...



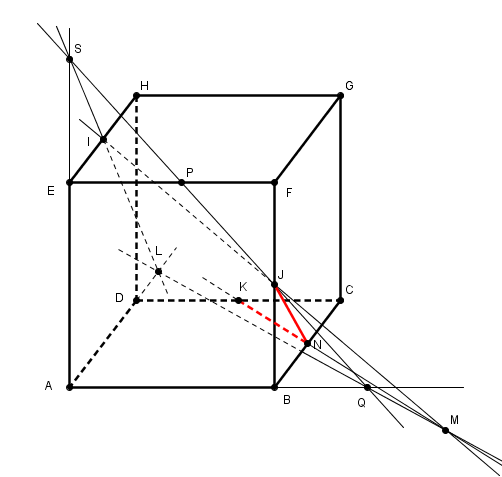
P et Q arbitraires jouent le rôle de B et F (du moment que P, J, Q alignés et dans le plan (ABFE))
la construction est alors la même que celle effectuée mais sans utiliser aucune parallèle donc aucun "théorème d'incience" du tout.


pas sûr que c'est ce qu'ils attendaient en disant "sans le théorème d'incidence" ...

Pour le théorème d'incidence, je ne sais pas pourquoi j'ai écrit parallèle je voulais dire sécant (on va mettre ça sur le dos de la fatigue couplée à un gros mal de tête).

A force de persévérer une bonne partie de l'après-midi, j'ai réussi à arriver au deuxième dessin de ton message juste avant votre réponse.

Merci beaucoup pour votre aide et bonne soirée.

Enfin pour dire vrai, j'étais presque arrivé au dessin que vous avez posté, mais je n'avais pas réussi à terminer la section (j'avais du mal à placer le point P).

Encore merci

attention P ne fait pas partie de la section du tout
c'est un point arbitraire qui sert à faire la construction sans utiliser du tout à aucun moment le théorème d'incidence.
ce qui n'était pas le cas de ton dessin.

mais on en est exactement au même point ni plus ni moins avec ton dessin (qui utilise le théorème pour construire L !!! )
et avec le mien (qui ne l'utilise pas) :
la construction du point N et c'est tout.

le seul point en dehors de I, J et K qui est connu de la section à cette étape c'est le point N
(le bout de la section connu à cette étape est uniquement ce qui est en rouge)

la suite de la construction c'est comme j'ai dit :

Pour trouver l'intersection de (KN) avec (ADHE), il faut prolonger les segments [KN] et [AD]. On note par exemple X le point d'intersection. Ensuite on trace le segment [IX] et on note Y le point d'intersection avec [HD]. On peut tracer [IY] et [YK] qui font partie de l'intersection non ?

Ce qui donne ceci

Est-il correct de faire ceci pour terminer la section ?

[PJ] et [PI] sont en continus, pas en pointillés (petite erreur d'étourderie)

c'est tout bon si tu acceptes d'utiliser une fois le théorème d'incidence pour tracer (IL) et déterminer ainsi le point L au début de la construction.

(IL) est parallèle à (BF) grâce au "théorème d'incidence", intersections des deux plans parallèles (BCGF) et (ADHE) avec le plan sécant (BFI)

le meilleur moyen de ne pas être accusé de l'utiliser en douce sans le dire est de ne JAMAIS tracer aucune parallèle à quoi que ce soit

c'est à dire de commencer par ma construction avec un plan auxiliaire (IJQ), Q complètement arbitraire sur (AB), "complètement de biais" au lieu de (IJB) (le point P que j'avais tracé n'a aucun rapport avec ton point P)

une fois N obtenu c'est la suite comme tu viens de le faire.