Inscription / Connexion Nouveau Sujet
Section du cube par un plan P
Bonjour, j'ai un devoir à rendre pour la rentrée dans lequel on me demande de tracer la section du cube ABCDEFGH par un plan P qu'on considère dans le repère (D; 1/4 DA; 1/4 DC; 1/4 DH).
On connait l'équation de ce plan : -6x+2y-3z+6=0 et ABCDEFGH est un cube d'arête 4.
J'aurais aimé un peu d'aide étant donné que je ne vois pas trop commencer.
Merci d'avance 
Bonjour
tu peux chercher des points du plan qui sont sur les arêtes de ton cube
éventuellement si besoin des droites d'intersection avec certaines faces du cube
Il n'y pas plus rigoureux que de chercher un peu hasard les points du plan qui sont sur les arêtes du cube ? Une méthode ou une démarche à suivre ?
Bonjour,
on ne les cherche pas "au hasard" mais par le fait que l'axe des x par exemple est (y = 0, z = 0) ...
Je remarque d'ailleurs que la deuxième solution n'en est pas vraiment une étant donné que x y et z sont compris entre 0 et 4 non ?
ça serait bien de leur donner des noms à ces points pour pouvoir continuer à en parler
par exemple, de la droite qui joint le point sur l'axe x avec le point sur l'axe y,
vu que cette droite est la droite d'intersection du plan donné avec le plan (xOy) alias (ADC)
ainsi que des noms aux autres points qu'on serait éventuellement amené à considérer sur cette droite là (intersections de cette droite avec des arêtes du cube par exemple)
nota : les axes ne sont pas limités au morceaux = une arête du cube
un plan et une droite étant infinis, il y a des parties peut être tout à fait intéressantes en dehors du cube !!
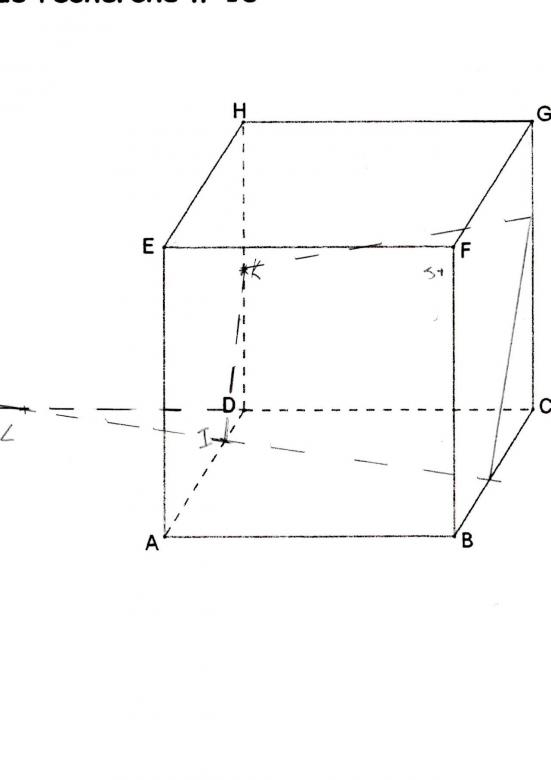
Je note I(1;0;0) et K(0;0;2), je dispose donc déjà d'une droite du plan P.
Mais ensuite j'ai du mal à me représenter le reste et je n'ai pas d'outils informatique sous la main...
"je n'ai pas d'outils informatique sous la main..."
ça n'empêche absolument pas de faire un croquis à main levée ne serait-ce que pour éviter de se mélanger les pinceaux !
il faudra aussi le 3ème point, si, si, relire mon nota
tu peux sur ce croquis à main levée reporter les 3 points obtenus et poursuivre la construction par le seul tracé géométrique (sans aucun autre calcul)
et je répète : les droites et pas seulement les segments.
et / ou bien calculer les coordonnée des divers points ainsi obtenus sur les arêtes du cube.
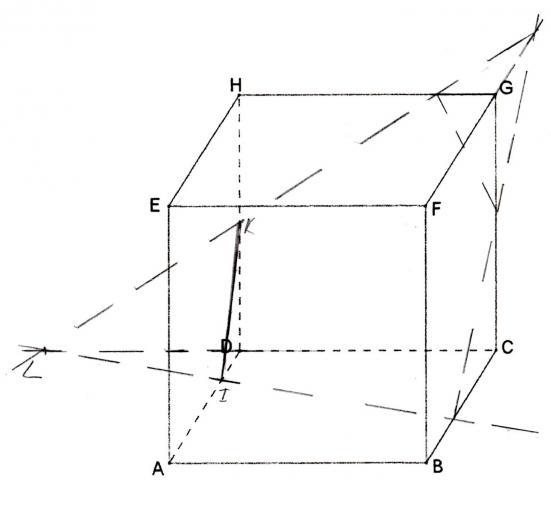
ta droite sur la face DCGH est "visiblement" fausse car elle doit passer par le point (0; -3; 0) vu que ce point, qui appartient à (P), est aussi dans ce plan (DCGH)
ton truc marqué "J +" représente quoi ?
le point (0; -3; 0) tu l'as appelé L ? (pas net)
Effectivement le point (0;-3;0) je l'ai noté L et le point J (ce n'est pas un "+" simplement une croix pour le situer) représente un autre point appartenant à P de coordonnées (1;3;2). J'avoue qu'il ne sert pas ici mais l'ayant trouvé je l'avais juste placé sur la figure  .
.
un point situé "en plein espace" ne sera pas très utile effectivement 
c'est pour ça qu'on a choisi de tracer des points sur les axes, et pas "n'importe où".
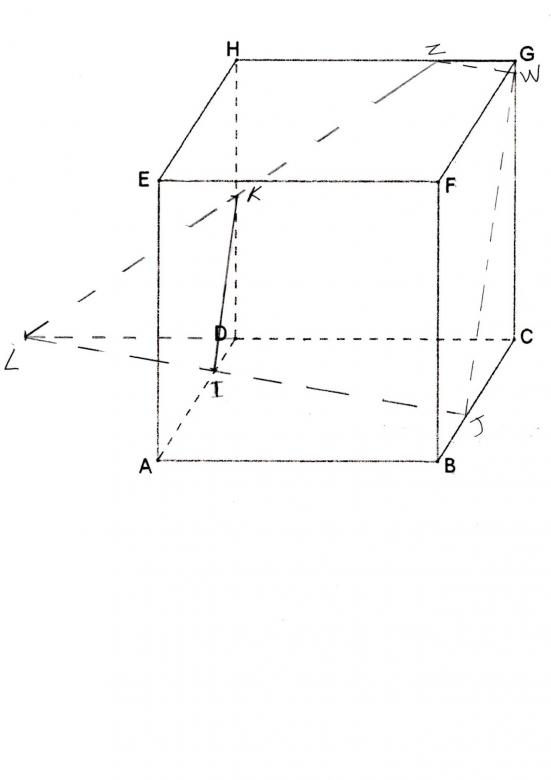
par contre tu dois corriger ta section comme je l'ai dit : la droite d'intersection du plan (P) et du plan (DCGH) est la droite (KL)
et par conséquent la section du cube par ce plan (P) n'est pas un quadrilatère mais un pentagone (irrégulier)
ton intersection avec BCGF est "un peu fausse" aussi
(imprécision du tracé de parallèle à (IK), ou de va savoir ce qui t'a permis de la tracer)
avec des noms de points pour tous les points de la figure ce serait plus facile de parler de quelles droites sont fausses sur ton schéma !
en tout cas la droite (KL) ne coupe pas du tout la droite (FG) (dans l'espace) :
la droite (KL) est entièrement dans le plan (DCGH)
si jamais elle coupait la droite (FG), ce serait en le seul point commun entre cette droite (FG) et le plan (DCGH) : le point G lui-même
or elle ne passe "visiblement" pas par G. (K,L,G pas alignés, on peut le prouver en justifiant que G ne fait pas partie de (P))
en faisant un dessin précis, W est sur [FG] et pas sur [CG]
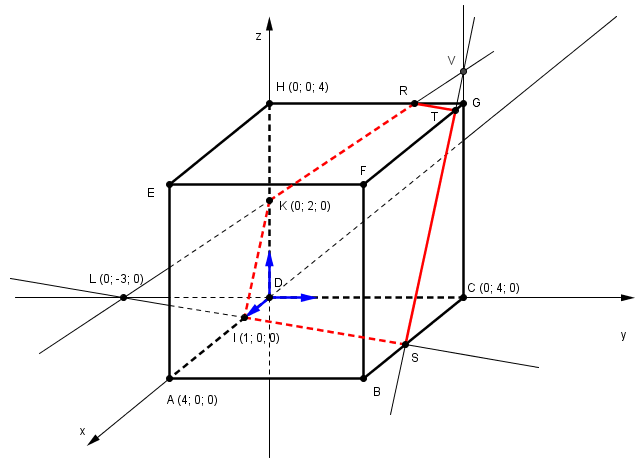
on peut le calculer en calculant l'intersection du plan (P) avec la droite (CG) (point V) pour savoir si son z > 4 ou < 4