bonjour ,
je ne pense pas que ce soit possible d'avoir un solide ayant un disque, un triangle et un caré sous des vues différentes

par contre, moi, personnellement, si tu prends ton cône suffisament petit, il peut passer au travers du trou représenté par un carré (on ne demande pas d'avoir une face un carré )

voilà
désolée, de ne pouvoir en trouver un correct, mais j'imagine mal, comment tu pourrais en fabriquer un

Bonjour,
A priori si le livre ne se trompe pas c'est possible.

Bonjour,

cercle : cylindre, cône, sphère.
carré : pyramide régulière de base carrée, pavé droit de base carrée (le cube est de la famille)
triangle : pyramide régulière de base triangulaire, prisme droit de base triangulaire.

Voici l'énoncé exact :
"Dans un livre de 1938, on peut lire l'exercice suivant :"Un carton est percé de trois ouvertures ayant respectivement la forme d'un triangle équilatéral, d'un carré et d'un cercle, les côtés des deux premiers et le diamètre étant égaux.
Trouver un solide, qui présenté de facons différentes puisse passer par ces trois formes en les épousant."

Source : rallye des maths, Bretagne

Bonjour Dasson, et les trois en même temps ?

c possible g trouvé comment il fo faire
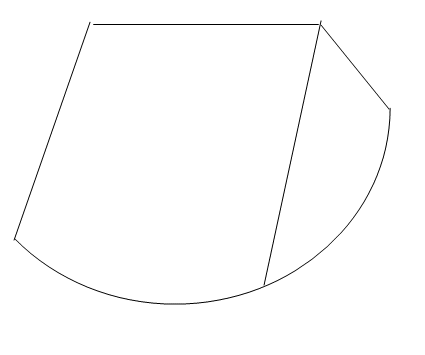
prend comme vu de face un carre comme vu de cote un triangle et comme vu de dessus un cercle

une petite image peut etre pas mal pour le voir

Bien vu !

EN perspective qqchose du type :

Merci

Philoux

pas mal, j ai pas reussi a faire un truc aussi bien sous paint

>Avce word

Mais je dois t'avouer, de passer de ta réponse à la mienne, j'ai eu du mal

Philoux

Bonsoir !

Si tu connais Pov-Ray, voici le code qui te permettra de visualiser la bestiole , il te suffira de changer la position de la camera.
J'ai mis en commentaires les positions qui permettent de voir le triangle, le carré et le cercle.

#include "colors.inc"

camera {
orthographic
//  location <5, 0, 0>
//  location <0, 0,5>
//  location <0, 5,0>
   location <1, 4,4>
  
   look_at <0,0,0>
}


background { color rgb <0, 0, .5> }
                  
light_source {
    <15, 80, 40>
    color White
}


#declare cyl=object{
intersection{
object{
intersection{
cylinder {
<0,0,0>,<0,2,0>,1
}

plane {
<4,2,0>,(2/sqrt(5))
}
}
}
plane {
<-4,2,0>,(2/sqrt(5))
}
pigment{ color rgb <1,1,0>}
}}


object{
cyl
}

        




_____________________
Je suis nul en maths.

reBonsoir !

Si tu ne connais pas, voici quelques aperçus. Désolé pour la qualité de l'image, mais le format GIF généré par Paint n'est pas top.

_____________________
Je suis nul en maths.

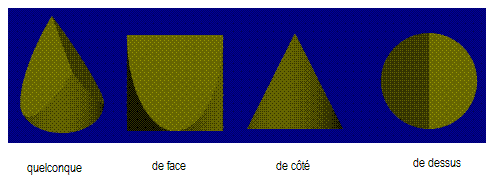
Superbe N_comme_Nul !

La qualité de l'image est largement suffisante pour "visualiser" le résultat !

Je ne connais pas Pov Ray (et ne peut pas trop surfer) : c'est un freeware, GNU ?

Merci pour l'aperçu.

Philoux

Fantastique !

C'est joli les maths non ?

Merci à tous

Bonjour !

Tout à fait philoux. C'est encore mieux qu'un freeware, c'est un opensource.

Téléchargeable gratuitement (Windows, Linux, Mac) :
                      http://www.povray.org/


_____________________
Je suis nul en maths.

Merci N_comme_Nul (tu mérites mieux que ton pseudo, même au 2° d° )

L'utilises-tu sous Win : PovWin V3.6 ?
ou sous un autre OS ?

Merci encore, c'est sympa

Philoux

Bonsoir !

Tout dépend sous quel OS je me trouve

J'en utilise deux : XP et Linux Fedora Core 3.

Mais j'ai Pov Ray sous les deux.

Voili voilà.

_____________________
Je suis nul en maths.

>N_c_N

Alors, si tu connais sous Win, quelle est la dernière version stable ?
c'est une béta ?

Y-a-t-il une doc en Français (en vue diffusion élèves), ou un tutorial F ?

Sinon, connais-tu des équivalents de PovRay en F ?

Merci pour toutes ces réponses; je quitte l' pour ce WE.

Bon WE à tous

Philoux

reBonsoir !

Désolé de ne pouvoir te répondre pour ce qui est "du français" (j'y suis allergique).

Il y a par contre un éditeur KPovModeler sous Linux (pas besoin de connaître toute la synthaxe de Pov-Ray), mais je ne pense pas qu'il y ait un équivalent sous Windows.

Moi, je suis autodidacte sous Pov Ray et j'ai tout appris à partir des documentations officielles et je tape toutes les commandes à la main, comme sous LaTeX pour mes documents perso.

Assez intuitif d'ailleurs, genre pour définir un plan : il faut un vecteur normal et une distance d'éloignement par rapport à l'origine etc.

Pour la "bestiole", quelques petites opérations booléennes ... comme intersection d'un cylindre et de deux plans.

Pour des tutoriaux en français ... ça doit exister, mais préfère ceux en anglais .

Google est ton ami.

Salut, et bon week-end.

_____________________
Je suis nul en maths.

reBonsoir !

essaie :

http://www.linuxgraphic.org/section3d/povray/

section "Les didacticiels"

A+
_____________________
Je suis nul en maths.

Bonjour,

Ce petit problème continue de m'intéresser.

L'ayant soumis à d'autres personnes (jeunes pas trop familiarisés avec la représentation spatiale, et moins jeunes aussi ), j'ai décidé de réaliser cette pièce en bois pour montrer sa faisabilité (beaucoup ont du mal à voir, certains doutent !).

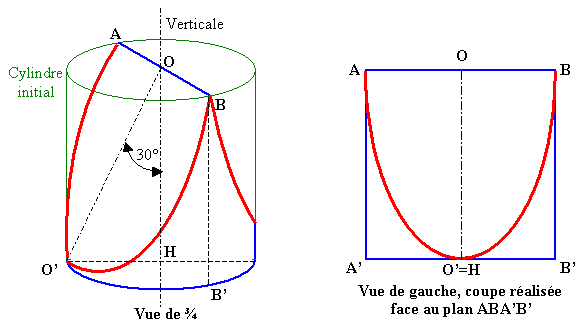
Il s'agirait donc d'un cylindre de hauteur=(racine(3)/2).diamètre, sur lequel on effectue deux tranches symétriques partant d'un même diamètre et inclinées à +/- 30° par rapport à la verticale (le dessin ci-dessous tente de visualiser cette phrase absconse).

Les questions pour lesquelles je sollicite votre aide sont les suivantes :
Quelle est la nature de la courbe rouge quand on la regarde en étant dans un plan // ABA'B' ?
Je crois que c'est une conique : arc parabole ou hyperbole ?
Y a-t-il un moyen (pas trop mathématique, ou accessible niveau Bac-) de le démontrer et d'obtenir l'équation de la courbe rouge projetée dans le plan ABA'B' ?

Merci pour votre aide et bon week-end,

Philoux

Autre question :
Si on prend l'énoncé initial, "côté du triangle équilatéral = côté du carré"; la solution proposée n'y répond pas puisque la hauteur du triangle (base x racine(3)/2) doit être égal au côté du carré, donc à la base !
A moins de faire entrer, dans le trou carré, la pièce inclinée ? non pas dans le plan ABA'B' mais dans le plan ABO' ?
Qu'en pensez-vous ?

Bonjour !


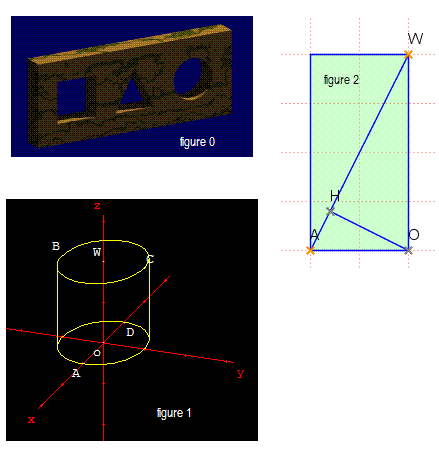
En fait, je suis parti d'un cylindre de rayon et de hauteur . (voir figure 1)
Le carré ainsi obtenu a un côté de et le triangle une hauteur de aussi (les côtés de même longueur ont de côté, la base de ) (voir figure 0).

(Je n'avais pas lu les consignes "exactes" indiquées par bonjour
dans le post du 30/05/2005 à 17:13, je n'ai donc pas pris un triangle équilatéral ... ).

Ce cylindre, je l'ai coupé par deux plans et d'équations respectives et . (voir figure 1)

Sous Pov-Ray, on définit un plan par un vecteur normal et une distance de séparation par rapport à l'origine. Un petit coup de produit vectoriel et on en parle plus () pour , et pour , il suffit de prendre le symétrique de ce vecteur par rapport au plan .

Reste à déterminer la distance de séparation. Cela revient à résoudre un petit problème niveau collège (voir figure 2).
On trouve que .


Tout ceci est ajustable pour le cas d'un triangle équilatéral .

Pour ce qui est de la courbe rouge, je pense qu'il faut reconnaître, après projection sur quelque chose du genre
    
à partir de
    




_____________________
Je suis nul en maths.

reBonjour !


Avec l'équation que je donne dans mon post précédent, ça devient indépendant de la variable et c'est bien la forme de l'équation d'une ellipse (d'un morceau d'ellipse).

_____________________
Je suis nul en maths.

bonjour ,
logique que ce soit une ellipse (il y a des tangentes au point O', A et B (enfin pour ces derniers, des demi-tangente )
pour ce qui est de l'objet, j'avais du mal à l'imaginer ainsi, mais il est vrai que je suis trop bornée sur les solides connues

bonne continuation

Salut muriel,

Comment peut-on (pouvait-on) être certain que ces 1/2 tgtes sont (étaient) verticales ?

>merci à NenM pour ce développement; malheureusement, l'investissement pour utiliser PovRay me rebute qq peu, alors que l'outil semble très riche. Peut-être plus tard...

Pour la démo "accessible" de l'ellipse (puisque s'en serait-une), vous n'avez rien de plus ... facile ?

Merci encore

Philoux

>NenM : utilises-tu PvRay à des fins professionnelles ?
si oui (ou non d'ailleurs), connais-tu les réglementations d'utilisation de ce type de soft à des fins professionnelles ?

Merci

c'est en fait une conjecture que j'ai faite
mais si tu coupes ton solide un peu plus bas, là ou il n'y a pas de tangentes verticales (si tu le pose sur le face du disque) , tu obtiens quoi sur le face du triangle? un trapèze, non?

ensuite, tu dois surement savoir que l'inrsection d'un cylindre avec un plan est soit un rectangle (lorsque le plan est perpendiculaire à la base)
soit un disque ou un cercle (si le plan est parallèle à la base)
soit une ellipse (si le plan n'est ni perpendiculaire, ni parallèle à la base)

Bonjour muriel,

ensuite, tu dois surement savoir que l'inrsection d'un cylindre avec un plan est soit un rectangle (lorsque le plan est perpendiculaire à la base

Si tu le dis...J'ai du l'apprendre

Philoux

il suffit que tu observes cela pour t'en rappeler

bonne journée

Bonsoir !

philoux > Je n'utilise pas Pov-Ray à des fins professionnelles, bien que je le pourrais . Je l'ai toujours utilisé par curiosité.
Quelques exemples sur mon "site" ( quand est-ce que je vais m'y mettre pour le mettre à jour ? )
                  

Comme c'est un logiciel open source, on peut l'utiliser à loisir. Mais s'il s'agit d'une utilisation à but lucratif, je ne sais pas.
Je peux te conseiller peut-être d'aller sur le forum du site de Framasoft, dans la rubrique juridique.
                  



_____________________
Je suis nul en maths.

slt N_comme_Nul

un fan de Naruto ?

+

Salut H_aldnoer

La curiosité est un des plus beaux défauts ... mais seulement en maths. (je rigole)

Et pour répondre : pas vraiment, il s'agit en fait d'un avatar que j'avais confectionné pour une contact. Voili voilà.

_____________________
Je suis nul en maths.

re

dommage tu c pas ce que tu rate

sinon j'adore ce que tu fait

ac Pov-Ray ?

facile d'utilisation ?

_{(ca fait longtemps que je n'ai plus fait de 3D ... c'etait ac Maya)}

re

Merci H_aldnoer .

Je crains que mes posts sont en train de "dériver" (aucun contenu mathématique).

Mes images en 3D faites sous Pov-Ray sont des essais (faits pendant mes vacances). Pour ce qui est de la facilité d'utilisation ... euh disons qu'il faut taper un script qui permet au moteur de rendu de générer l'image. Pour ce qui est de la facilité, je répondrais non. Mais c'est ce que je préfère . Sous Linux, il existe un soft KPovModeler qui permet de s'affranchir de ces scripts. (Cet été je vais me remettre à Blender ... mais en pur amateur).
J'aime vraiment ce que font tous ces "génies" de la 3D ... je peux te suggérer d'aller voir le site de l'Internet Ray Tracing Competition :
      
pour admirer quelques chefs d'oeuvre.
Ce que j'aime bien avec Pov-Ray c'est qu'il peut gérer des objets infinis tels cylindre, plan ... et qu'avec de la patience on peut arriver à de belles images. Et les applications pour les mathématiques sont évidentes : on peut avoir de belles sections de solides (éventuellement texturés voire "atmosphérisés" [ avec un léger brouillard à l'intérieur] ) et des représentations d'objets de l'espace fidèles (je pense notamment à toutes les quadriques).

J'avais aussi (via de petits programmes en C++) généré des images du "problème de la vie" généralisé à des situations 3D. Chaque "pixel vivant" était représenté par une sphère (il faudrait d'ailleurs que je retrouve l'une de ces images pour la mettre sur mon site ).

Voila .
_____________________
Je suis nul en maths.