Inscription / Connexion Nouveau Sujet
Solution d'une équation 2
Bonsoir j'ai besoin de votre aide svp.
Exercice :
Une boîte cylindrique de rayon 12 cm contient de l'eau jusqu'à une hauteur de 5cm. On immerge une boule métallique dans ce récipient et on constate que la surface de l'eau est tangente à la boule . On désigne par x le rayon de la boule en millimètre.
1-a) Démontrer que 25 ≤ x ≤ 120.
B) Démontrer que x est solution de l'équation:
x³-21600x+540000=0 (E)
2-a) Démontrer que l'equation (E) admet deux solutions positives 
et 
tels que 
[25,6 ; 26] et [125 ; 135]
Je n'arrive à faire la démonstration de la première question.
Bonjour,
fatalement le diamètre de la boule sera supérieur à la hauteur d'eau initiale, puisque le niveau de l'eau va monter quand on met la boule, et que le diamètre de la boule sera cette nouvelle hauteur là
et il faut que ça rentre dans le récipient.
ce n'est que ça cette question
du simple bon sens pratique.
Ok. Le diamètre de la boule doit être inférieure ou égale à celui de la boîte cylindrique pour que la boule entre dans le récipient et vu que lorsque la boule est immergée dans le récipient , son diamètre est supérieur ou égal à la hauteur initiale d'eau.
On a donc :
5 cm ≤ 2x ≤ 2×12 cm
=> 5/2 cm ≤ x ≤ 12 cm
=> (5/2)×10 mm ≤ x ≤ 12×10 mm
=> 25 ≤ x ≤ 120
voila.
ensuite c'est ça :
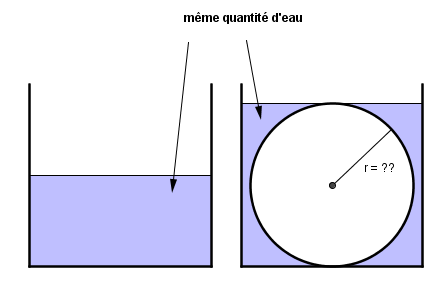
donc calculer la quantité d'eau initiale
et le volume total eau + bille si la hauteur est 2x
Quantité de initiale
Ve=πr²h=π(12×10)²×5×10=7,2.105π mm³
Volume eau + bille
V=πr²(2x)=π(120)²(2x)=28800πx
certes, mais il ne faut pas s'arrêter là !
ce volume eau +bille est aussi le volume d'eau (calculé précédemment) + le volume de la bille (formules de volumes) !!
et c'est cette égalité entre ces deux façons de calculer ce volume total qui donnera ce que demande la question 2b
Ok
Soit V' le volume de la boule
V=Ve+ V'
=> 28800πx=720000π+(4/3)πx³
=>(4/3)πx³-28800πx+720000π=0
=> x³-21600x+540000=0
2-a)
Soit f(x)=x³-21600x+540000
Df=[25 ; 120]
Pour tout x de Df , f'(x)=3x²-21600
Tableau de variation de f sur [25 ; 120]
f(60√2)=-86400√2+540000 < 0
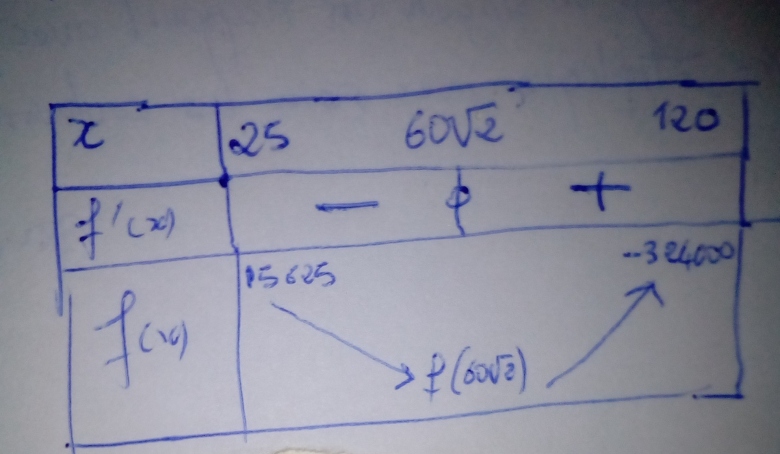
OK.
mais on te parle d'une solution [125 ; 135]
donc, il faut étudier f(x) sur un intervalle qui va jusqu'à x = 135, même si on a "restreint" le domaine de définition à l'intervalle pour lequel le problème physique a un sens (la boule tient dans le récipient), l'équation est à résoudre sur R tout entier.
de la façon dont est rédigé l'énoncé avec sa solution , c'est seulement ensuite, dans une conclusion finale de l'exo (une question 2b !) que l'on éliminera celles qui sont en dehors de [25; 120]
pour terminer la 2a on pourra utiliser le TVI
... à condition de connaitre les signes (donc de calculer) les valeurs de f(x) en chacune des bornes des intervalles de l'énoncé [25,6 ; 26] et [125 ; 135]
Il n'y pas de question 2-b qui nous permettrait d'éliminer les solutions en dehors de [25 ; 120] !
Voici le tableau de variation de f sur R
f(-60√2)=864000√2+540000 >0
f(60√2)<0
_ La fonction f est strictement continue et croissante sur ]-oo -60√2[ , et f(]-oo ; -60√2[)=]-oo ; f(-60√2)[ or 0 appartient à ]-oo ; f(-60√2)[
donc l'équation f(x)=0 admet une unique solution sur ]-oo ; 60√2[
De même 0 appartient à ]f(-60√2) ; f(60√2)[ et 0 appartient à ]60√2 ; +oo[ => f(x)=0 admet une unique solution sur ]-60√2 ; 60√2[ et une unique solution sur ]f(60√2) ; +oo[
En conclusion l'équation f(x)=0 admet trois solutions sur R
Je crois que le mieux ,c'est fa
dresser le tableau de variation sur [20 ; 135]
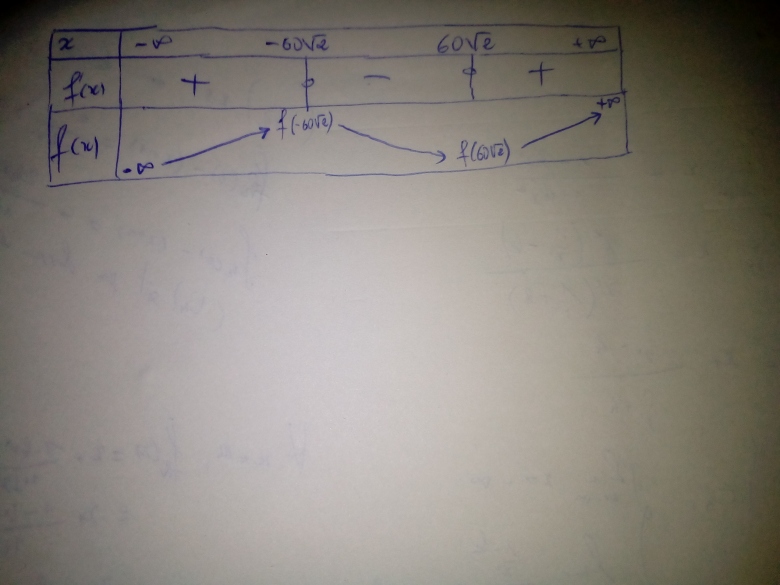
c'est juste sauf des erreurs que je qualifierais d'erreurs de frappe (des "f" là où ils n'ont pas lieu d'être ...)
mais tu ne réponds pas à la question
2-a) Démontrer que l'equation (E) admet deux solutions positives
et tels que [25,6 ; 26] et [125 ; 135]]60√2 ; +oo[ c'est grand !!
on demande de prouver que cette solution là est en fait dans [125 ; 135]
et de même pour celle dans ]-60√2 ; 60√2[ dont il faut prouver qu'elle et en fait dans [25,6 ; 26]
et j'ai dit comment : en calculant numériquement les valeurs de la fonction en ces bornes là.
quant à une question numérotée 2-a sans question 2-b ah! ah ! ah !
ou elle s'appelle 3 ou va savoir comment ou même sans aucun numéro,
la question qui permet de conclure sur la ou les valeurs du rayon de cette bille si on faisait véritablement cette expérience
et pas un calcul de brute déconnecté de la description initiale de cette expérience.
La question 2-b) est:
Déterminer alors une valeur approchée du rayon de la boule à 0,1 mm près.
Sinon je pense qu'il est préférable d'étudier f sur [20 ; 135]
On a :
_ f(25,6)≈3817 ≥ 0
f(26)=-4024 ≤ 0
Donc l'équation f(x)=0 admet une solution telle que
25,6 ≤ ≤ 26
_ f(125)=-206875 ≤ 0
f(135)=84375 ≥ 0
donc l'equation f(x)=0 admet une solution telle que
125 ≤ ≤ 135
l'étude se fait sur R
on en déduit que sur [25,6 ; 26] la fonction est décroissante
et que sur [125 ; 135] elle est croissante
et que pour savoir si dans ces intervalles là elle passe par 0
(c'est bien ce que demande la question ? Non ?
bein il faut calculer f(25,6) f(26) f(125 et f(135)
pour appliquer le TVI dans ces intervalles là (c'est l'énoncé )
2-b) est: ...
ah bein voila !!
c'est là qu'on détermine si les deux solutions alpha et beta dont on parle à la question d'avant conviennent ou pas
et il n'en reste qu'une, d'où la question (2b) :
une valeur approchée du rayon de la boule à 0,1 mm près.
et pas les valeurs approchées
et cela consiste à réduire l'intervalle dans lequel on a trouvé qu'elle était (la question d'avant) à une largeur < 0.1 mm
par la méthode que l'on veut
(tableur, calculette, programme de dichotomie, etc)
ce que tu dis dans la 2a c'est dans la 2b qu'il faut le dire
"vu que 25 ≤ x ≤ 120 donc la seule solution valable est alpha"
la 2a c'est juste ce qui est demandé dans la question 2a : l'existence de alpha et beta dans les intervalles indiqués et c'est tout.
le rapport avec le rayon de la bille, donc avec [25; 120], c'est au début de la 2b qu'il faut le faire
juste avant de balayer dans le seul intervalle contenant alpha.
sinon le résultat est correct.
Annuler
connectez vous