Inscription / Connexion Nouveau Sujet
Solution unique dans IR.
Bonsoir ,
Merci d'avance. 
1) Démontrer que l'équation admet une solution unique
dans tel que -4 <
< -3.
2) Donner une valeur approchée de à près :
a-) En utilisant la méthode par balayage.
b-) En utilisant la méthode par dichotomie.
Réponses
1) , soit
.
f est dérivable sur .
Donc ,
,
.
Donc f est strictement croissante sur [-2;1] et strictement décroissante sur ]-∞ ;-2] U [1 ;+∞[.
Je ne vois pas comment faire ensuite.
Comme , f est continue et strictement décroissante sur [-4 ; -3].
f(-3) × f(-4) = -18 × 23 = -414 < 0.
D'après le théorème de Corollaire , f admet une solution unique dans ]-4 ;-3[.
D'où -4 < < -3.
Je ne vois pas comment utiliser le taux de variation là si j'ai bien compris
Salut,
(en l'absence de carpediem ) :
Ilme semble qu'il faut tout de même étudier la fonction sur IR (cf question posée : 1)
Démontrer que l'équation
dans < -3.Ensuite :
Revois ton cours, "D'après le théorème de Corollaire " ne veut rien dire.
Enfin :
Je ne vois pas comment utiliser le taux de variation là si j'ai bien compris
Yzz : oui tu peux !!! bien sûr ...
je me concentrais essentiellement sur l'intervalle [-4, -3] mais tu as bien sur raison ... il faudra justifier qu'il n'y en pas ailleurs
PS : je poserai bien entendu f(x) = 2x^3 + 3x^2 - 12x + 9 pour éviter tous ces signes et parce que -a = 0 <=> a = 0
...
"une unique solution sur IR ; et cette solution est entre -4 et -3.
Ok.
Revois ton cours, "D'après le théorème de Corollaire " ne veut rien dire.
C'est écrit là '' Corollaire'' , je ne vois pas comment énoncé ce théorème d'une autre manière.
Que vient faire ici un "taux de variation" ?
Dans ce cas j'ai mal compris ceci.
ensuite utilise le "TVI" !!
C'est écrit là '' Corollaire'' , je ne vois pas comment énoncé ce théorème d'une autre manière.
Que vient faire ici un "taux de variation" ?
Dans ce cas j'ai mal compris ceci.
ensuite utilise le "TVI" !!
Pour la question 1) , est il nécessaire de déterminer f(]-∞ ; -2[) ?
2) Je fais comment ?
Pour la question 1) , est il nécessaire de déterminer f(]-∞ ; -2[) ?
Ok , mais je ne comprends pas pourquoi on devrait le faire..
2) on peut avoir
= 3,1.
Mais comment trouver cela par ces deux différentes méthodes que je ne retrouve pas ?
On te demande de justifier que f(x) = 0 admet une unique solution sur IR.
Il te faut donc étudier la fonction sur IR, pas seulement sur [-4;-3].
2) on peut avoir
= 3,1.Trouvé comment ?
On te demande de justifier que f(x) = 0 admet une unique solution sur IR.
Il te faut donc étudier la fonction sur IR, pas seulement sur [-4;-3].
Pourtant c'est bien ce que je croyais faire :
1)
f est dérivable sur
Donc
Donc f est strictement croissante sur [-2;1] et strictement décroissante sur ]-∞ ;-2] U [1 ;+∞[.
Comme
f(-3) × f(-4) = -18 × 23 = -414 < 0.
D'après le Corollaire du théorème des valeurs intermédiaire , f admet une solution unique dans
< -3.
Je ne comprends pas pourquoi je devrais calculer f(]-∞ ;-2[)
Tu n'as fait que prouver que f(x) = 0 a une unique solution sur [-4 ; -3] , tu n'as pas prouvé qu'il n'y en avait pas une autre ailleurs.
Donc : fais ton tableau de variation complet sur IR, et prouve que f ne s'annule pas ailleurs que sur [-4 ; -3].
1) , soit
.
f est dérivable sur .
Donc ,
,
.
Donc f est strictement croissante sur [-2;1] et strictement décroissante sur ]-∞ ;-2] et sur [1 ;+∞[.
* Tableau de variation de f.
,
,
et
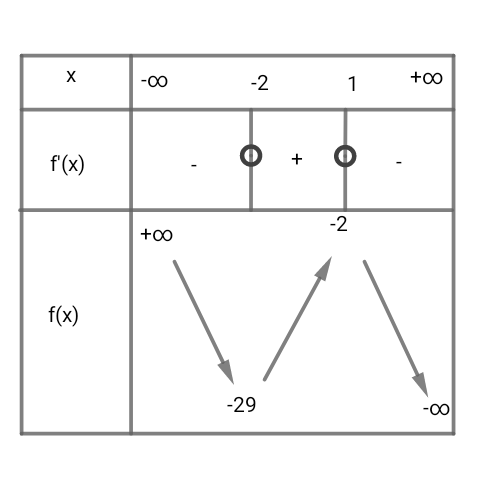
* Comme , f est continue et strictement décroissante sur [-4 ; -3].
f(-3) × f(-4) = -18 × 23 = -414 < 0.
D'après le Corollaire du théorème des valeurs intermédiaire , f admet une solution unique dans tel que
]-4 ;-3[ ou encore -4 <
< -3.
* f est continue et strictement décroissante sur ]-∞ ; -2] et f(]-∞ ; -2])= [-29 ; +∞[.
0 et -4 et -3 [-29 ; +∞[ , donc f(x)=0 admet une solution unique
dans ]-∞ ;-2] tel que -4 < < -3.
* f est continue et strictement croissante sur [-2 ;1] et f([-2 ;1])= [-29 ;1].
0 , -4 et -3 [-29 ;1] , donc f(x)=0 admet une solution unique dans [-2 ;1] tel que -4 <
< -3.
Par conséquent , f(x)=0 admet une solution unique dans tel que -4 <
< -3.
Non.
Tu n'as visiblement pas compris le fond du problème.
Pour montrer que f(x) n'a qu'une seule solution dans IR (qu'elle soit dans [-4 ; -3], on verra après) :
- Tu montres qu'il n'y en a qu'une seule dans ]-oo ; -2] en appliquant le corollaire du TVI
- Tu montres qu'il n'y en a pas d'autre ailleurs, c'est à dire dans [-2;+oo[
Enfin, tu prouves que cette solution est dans [-4 ; -3].
1) , soit
.
f est dérivable sur .
Donc ,
,
.
Donc f est strictement croissante sur [-2;1] et strictement décroissante sur ]-∞ ;-2] et sur [1 ;+∞[.
* Tableau de variation de f.
,
,
et
* f est continue et strictement croissante sur [-2 ;1] et f([-2 ;1])= [-29 ;-2].
0 [-29 ;-2] , donc f(x)=0 n'admet aucune solution dans [-2 ;1].
*f est continue et strictement décroissante sur [1 ;+∞[ et f([1; +∞[)=]-∞ ;-2].
]-∞ ;-2] , donc f(x)=0 n'admet aucune solution dans [1 ;+∞[.
Par conséquent , f(x)=0 admet une solution unique dans .
* f est continue et strictement décroissante sur ]-∞ ; -2] et f(]-∞ ; -2])= [-29 ; +∞[.
0 [-29 ; +∞[ , donc f(x)=0 admet une solution unique
dans ]-∞ ;-2].
Par conséquent , f(x)=0 admet une solution unique dans .
* Comme , f est continue et strictement décroissante sur [-4 ; -3].
f(-3) × f(-4) = -18 × 23 = -414 < 0.
D'après le Corollaire du théorème des valeurs intermédiaire , f admet une solution unique dans tel que
]-4 ;-3[ ou encore -4 <
< -3.
on peut faire plus simple (que ce travail trop mécanique) :
le maximum de f sur l'intervalle [-2, +oo[ est -2 donc l'équation f(x) = 0 n'a pas de solution sur cet intervalle.
f est strictement décroissante de ]-oo, -2] sur [-29, +oo[ et 0 appartient à cet intervalle.
donc d'après le TVI l'équation f(x) admet une unique solution dans l'intervalle ]-oo, -2]
or f(-4) = ... et f(-3) = ... donc f(-3) < 0 < f(-4)
donc la solution de l'équation f(x) = 0 appartient à l'intervalle [-4, -3]
le maximum de f sur l'intervalle [-2, +oo[ est -2 donc l'équation f(x) = 0 n'a pas de solution sur cet intervalle.
Le minimum ?
f est strictement décroissante de ]-oo, -2] sur [-29, +oo[ et 0 appartient à cet intervalle.
Oui , je vois bien la bijection réciproque de f.
donc d'après le TVI l'équation f(x) admet une unique solution dans l'intervalle ]-oo, -2]
or f(-4) = 23 et f(-3) = -18 donc f(-3) < 0 < f(-4)
donc la solution de l'équation f(x) = 0 appartient à l'intervalle [-4, -3]
Je n'ai pas bien compris.
Toujours en accord avec carpediem ( (
) , je reprends tes remarques :
Le minimum ?
Et si le minimum était -2 , comment affirmer alors que f(x) = 0 n'a pas de solution ?
"le maximum de f sur l'intervalle [-2, +oo[ est -2 " signifie que f(x)
-2 sur [-2, +oo[ ... et donc f(x) = 0 ...etc ...
Oui , je vois bien la bijection réciproque de f.
Je n'ai pas bien compris.
Mais cette "méthode" ne s'applique que pour l'équation f(x) = 0 , alors que le TVI est valable pour toute équation du type f(x) = k compris entre f(a) et f(b).
Par exemple dans ton exercice, on aurais pu te demander de prouver que l'équation f(x) = 12 admet une unique solution dans IR : tu ne t'en serais pas sorti avec un "f(a)*f(b) = k" (sauf à changer de fonction naturellement).
Bonne journée
Bonjour,
Je crois que le sujet est plus ou moins clos.
Je me permets donc d'intervenir sur
Pour la question 1) , est il nécessaire de déterminer f(]-
; -2[) ?La fonction est décroissante sur ]-
; -2[ ; donc si Vu que f(-4) = 23, on a f(x) non nul si x < -4.
Bref, les limites en
ne sont pas nécessaires.
Sur [-4;-3], on utilise une conséquence (corollaire) du théorème des valeurs intermédiaires.
Ailleurs, c'est du niveau classe de seconde.
Il n'est pas interdit de s'appuyer sur un second tableau de variation en y insérant -4 et -3 dans la ligne des x, et 23 et -18 dans la flèche descendante de gauche.
Annuler
connectez vous