Inscription / Connexion Nouveau Sujet
somme vecteur 4
Bonsoir, mon exercice est-il juste, merci.
On considère les trois points suivants :
A(2 ; 1) ; B(−1 ; 3) ; C(0 ; −2)
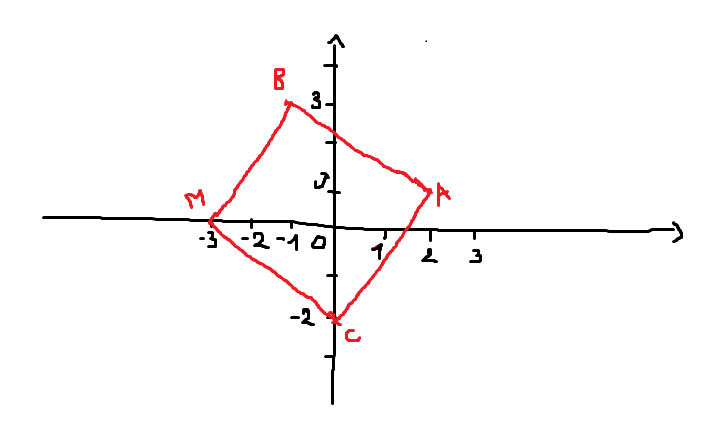
1. Placer les points A, B et C.
2. Calculer les coordonnées du vecteur→AB.
3. a. Déterminer les coordonnées du point M afin que le quadrilatère ABMC soit un parallélogramme.
b. Tracer le parallélogramme ABMC.
voici mes réponses :
1. voir le graphique.
2. Calculer les coordonnées du vecteur →AB :
A (2;1) et B (-1;3)
→AB (xA-xB) et (yA-yB)
→AB (-1-2) et (3-1)
donc, AB (-3;2)
3. a. Déterminer les coordonnées du point M :
Soit K le milieu de la diagonale [BC].
On a B(-1;3) et C(0;-2)
xK = xB + xC/2 et yK = yB + yC /2
xK = -1 + 0/2 et yK = 3 + (-2) /2
xK = -1/2 et yK = 1/2
xK = -0,5 et yK = 0,5
Les coordonnées de K sont (-0,5 ; 0,5)
K est aussi le milieu de la diagonale [AM].
On a A (2;1) et K (-0,5 ; 0,5)
xK = xA + xM/2 et yK = yA + yM /2
-0,5 = 2 + xM/2 et 0,5 = 1 + yM/2
-1 = 2 + xM et 0,5 = 1 + yM
-1-2 = xM 0,5 - 0,5 = yM
-3 = xM et 0 = yM
Les coordonnées de M tel que ABMC soit un parallélogramme sont
(-3 ; 0).
b. Voir le parallélogramme ABMC sur le graphique.
Heureusement que vous ne faites pas ce que vous dites
vous avez écrit comme formule générale les coordonnées de
ABMC parallélogramme donc
écrivons l'égalité des coordonnées
D'accord pour les coordonnées de M
2. Calculer les coordonnées du vecteur →AB :
A (2;1) et B (-1;3)
→AB (xB-xA) et (yB-yA)
→AB (-1-2) et (3-1)
donc, AB (-3;2)
3. a ABMC parallélogramme donc CM = AB
etc.. je n'ai pas trop bien compris
ABCD est un parallélogramme si et seulement si
C'est aussi ce que l'on vous a dit dans un autre sujet
donc on a les coordonnées de on écrit les coordonnées de
en prenant x et y pour les coordonnées de M
puis on applique
J'arrête pour cette nuit.
d'accord,
3.a ABMC est un parallélogramme donc →CM = →AB
donc, on écrit l'égalité des coordonnées de →AB aux coordonnées de →CM, en prenant x = -3 et y = 2 pour les coordonnées de M puis les coordonnées de C(0 ; −2).
M (-3;2) et C(0 ; −2).
→CM (x'M-x'C) et (y'M-y'C)
→CM (0+(-3)) et (-2+2)
donc, M (-3;0)
Non On écrit les coordonnées de comme on a écrit les coordonnées de
.
Comme il n'y a pas d'ambiguïté et que l'on ne connaît pas les coordonnées de M on prend tout simplement et
. Les coordonnées de C sont données
On écrit maintenant l'égalité des vecteurs, c'est-à-dire celle de leurs coordonnées
enfin on résout ce système
On conclut les coordonnées de M sont
Calculer les coordonnées du vecteur →CM :
C (0;-2) et M (x;y)
→CM (xM-xC) et (yM-yC)
→CM (x-0) et (y-(-2))
→CM (x) et (y + 2)
→CM = AB ⇔ {x = -3 et y + 2 = 2
y = 2-2
y = 0
Les coordonnées de M tel que ABMC soit un parallélogramme sont (-3 ; 0).


