Inscription / Connexion Nouveau Sujet
Sphère passant par des points
Bonjour,
J'aurai deux questions concernants le centre et le rayon d'une sphère:
1) L'énoncé nous dit que la sphère S1 passe par les points A,B,C et M et il faut calculer le rayon et son centre.
2) Ensuite, dans la deuxième question, c'est une autre sphère S2 qui passe par les points A,B et C et tangente à la droite DG. Ici aussi il faut calculer le rayon et son centre.
Je bloque vraiment car je ne vois pas comment on peut définir précisément une sphère seulement en donnant quelques points par lesquels elle passe...
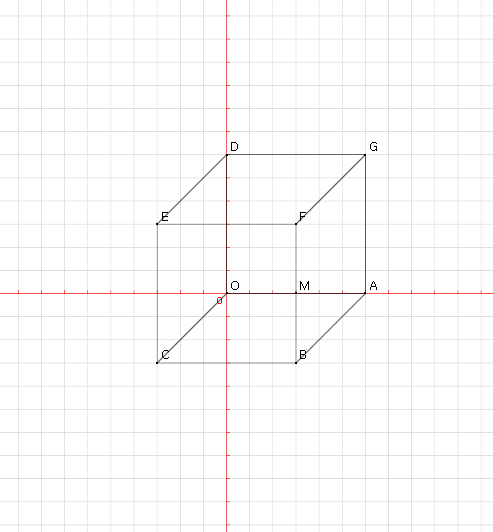
La figure qui nous est donnée est celle qui est ici-bas: il y a une axe des z normalement mais je n'ai pas su le tracer avec mon programme. ( l'axe des z passe par O et C )
Merci beaucoup de m'aider !!
salut
et un système d'équations?
quelle est l'équation d'une sphère si le centre a pour coordonnées (a;b;c) et le rayon r ?
comment, je ne vois pas...
L'équation d'une sphère qui a pour centre (a,b,c) comme rayon r, ça me fait beaucoup trop d'inconnues non ? Tu veux dire que apres avoir établi une éuation en fonction de a b et c et r ,je remplace par les points A, B et C ? Je ne suis pas sure de ce que tu veux dire...c'ets ça ?
Pour répondre à ciocciu, l'eq. c'est (x-a)2+(y-b)2+(z-c)2=r2.
Sinon, c'est obligatoire que le centre de la sphère se trouve sur le plan qui passe au milieu de M et B et parallèle au plan OABC.
pourquoi ce serait obligatoire que le centre de la sphère se trouve sur le plan qui passe au milieu de M et B et parallèle au plan OABC ?
Donc soit N le milieu de [MB] et de coordonnées (6; 6; 3/2).
Posons maintenant le point P, milieu de [OD] et de coordonnées (0; 0; 3).
Les points O et P appartiennent donc aussi à la sphère.
N et Q(0; 0; 3/2) forment une diagonale de la sphère S1.
Si c'est juste ce que je viens d'écrire, alors, ce n'est plus compliqué pour faire le reste.
Je viens de penser que le point N et Q sont un peu plus vers l'extérieur, vu qu'ils sont sur la diagonale, donc on ne connait pas les coordonnées exactes pour x et y.
J'ai pensé à une autre idée: premièrement étudier la droite d'intersection entre les plans médiateurs de AC et MB. Ensuite étudier le point d'intersection entre cette droite et le plan médiateur de CB.
Voila, je pense que cette méthode est juste mais je bloque sur un problème tout bête: je ne trouve pas de deuxième vecteur directeur au plans médiateur. Admettons que j'étudie l'équation du plan médiateur de AC, je trouve un seul vecteur: celui qui est le vecteur normal à la droite AC. Mais il m'en faut un autre et je ne vois pas comment le trouver !
Ce serait super de me débloquer la-dessus !
Merciii !!
et moi je persiste ....
on a 4 inconnues a,b,c et r
et on 4 points qui donneront donc 4 équations
donc on résout le système et on se prend pas trop la tête avec la géométrie
yek yek yek !

c'est bon, juste après avoir posté ce message j'ai réussi a me débloquer "toute seule" 
C'est tout simple car comme le vecteur normal de AC a pour coordonnées (admettons) (a,b,c), le plan médiateur a tout simplement une équation du type ax+by+cz+d=0
Aie aie aie je crois que c'est la fatique qui me fait pas penser à des choses toutes bêtes comme celle-ci tout de suite.
Merci quand même à vos réponses !!!
A+

 de coordonnées (3; 3; 3/2).
de coordonnées (3; 3; 3/2).
