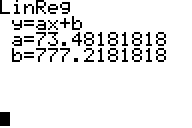Inscription / Connexion Nouveau Sujet
Statistiques avec nuage de points
Bonjour, je bloque sur ce dm je ne comprend vraiment rien du tout si quelqu'un aurait amabilité pourrait m'aider a le résoudre.
Le tableau ci-dessous indique l'évolution de la dette, en milliards d'euros, de l'état français entre 2000 et 2010.
Année Rang Dette en milliards d'euros
2000 0 827,3
2001 1 853,3
2002 2 912
2003 3 1004,9
2004 4 1079,5
2005 5 1147,6
2006 6 1152,2
2007 7 1211,6
2008 8 1318,6
2009 9 1492,7
2010 10 1591,2
1) L'accroissement annuel moyen de la dette est de 76,39 milliards d'euros pour la période 2000-2010. Justifier ce résultat.
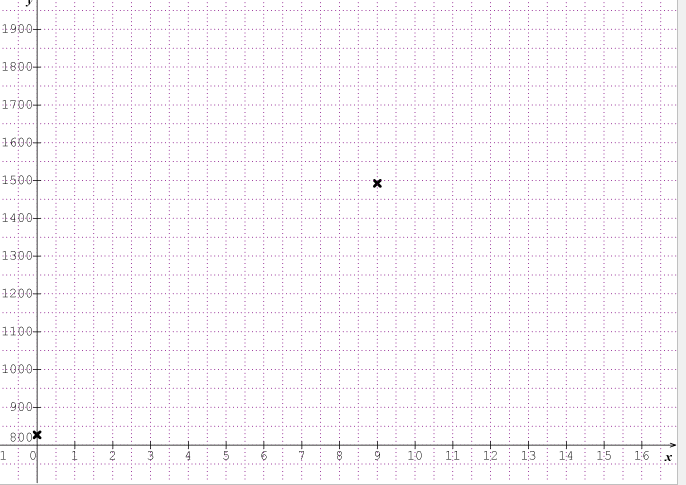
2) a) Représenter le nuage de points Mi(Xi;Yi) dans un repère d'unités 1 cm pour un an sur l'axe des abscisses et 1 cm pour 100 milliards d'euros sur l'axe des ordonnées, en commençant la graduation à 800 milliards d'euros.
b) La forme du nuage permet-elle d'envisager un ajustement affine? Justifier.
c) Calculer les coordonnées du point moyen G, arrondies à 0,1 près. Interpréter concrètement l'ordonnée de G.
d) Tracer la droite passant par G, de coefficient directeur 76,4. On précisera l'équation réduite de cette droite et les points utilisés pour la tracer.
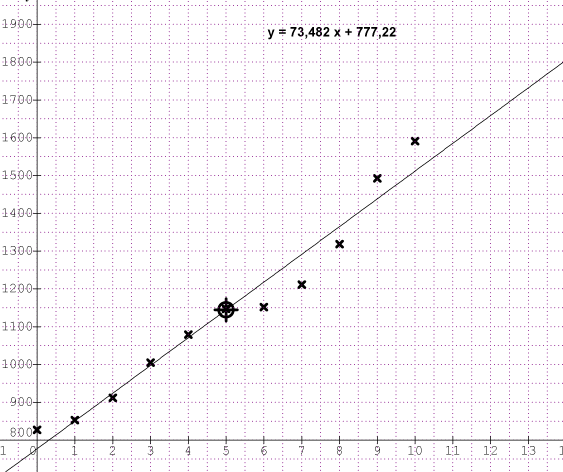
3) a) En utilisant la calculatrice, donner une équation de la droite de régression de y en x. Les coefficient a et b seront arrondis à 0,1 près.
b) Estimer le montant de la dette prévue pour l'année 2014 selon cet ajustement affine. L'estimation s'est-elle vérifiée ? Proposer une explication.
Aidez moi svppp !
bonjour
tu as le droit de faire des propositions.
1) L'accroissement annuel moyen de la dette est de 76,39 milliards d'euros pour la période 2000-2010. Justifier ce résultat.
Cela tu peux le justifier aisément
Bonjour,
Oui pour la question 1) j'ai mit (1591,2-827,3)/10=76,39
C'est la représentation graphique ou je n'y arrive pas
Merci de votre aide
Bonjour,
J'ai toujours eu un problème avec les repère et pour placer les points, pouvez vous m'aidez svp
Vous avez placé le point 827,3 et le point 1492,7 c'est bien ça ?
(vous avez fait le repère avec quel logiciel ?)
Merci de votre aide
Pas exactement puisque pour un point il faut deux coordonnées
donc
le logiciel est : sine qua non
Pensez à modifier votre profil vous êtes en seconde
De rien
Oui d'accord j'ai compris, j'ai essayer de faire le nuage de points sur feuille, je vois que les points sont à peu près alignés.
Le logiciel est en train de se telecharger je vous montrerais quand j'aurais tout finit.
Pour la question 2) b) On peut dire que le forme du nuage permet d'envisager un ajustement affine car les points sont alignés
Je ne sais pas bien justifier mais c'est à peu près ceci ?
Là aussi il faut nuancer . Tant que vous ne l'avez pas prouvé, vous ne pouvez l'affirmer.
Il semble que les points soient alignés mais là aussi ce n'est pas exact.
Écrivez plutôt les points semblent être dispersés concentrés (à choisir)selon une direction
Voilà j'ai trouver ça.
Je n'ai pas comprit comment je peut justifier..
Je suis désolée de vous dérangez, mais j'ai vraiment une mauvaise moyenne en math je suis obligé de demander de l'aide..
L'aide est faite pour que vous compreniez par conséquent vous pouvez poser autant de questions que vous voulez
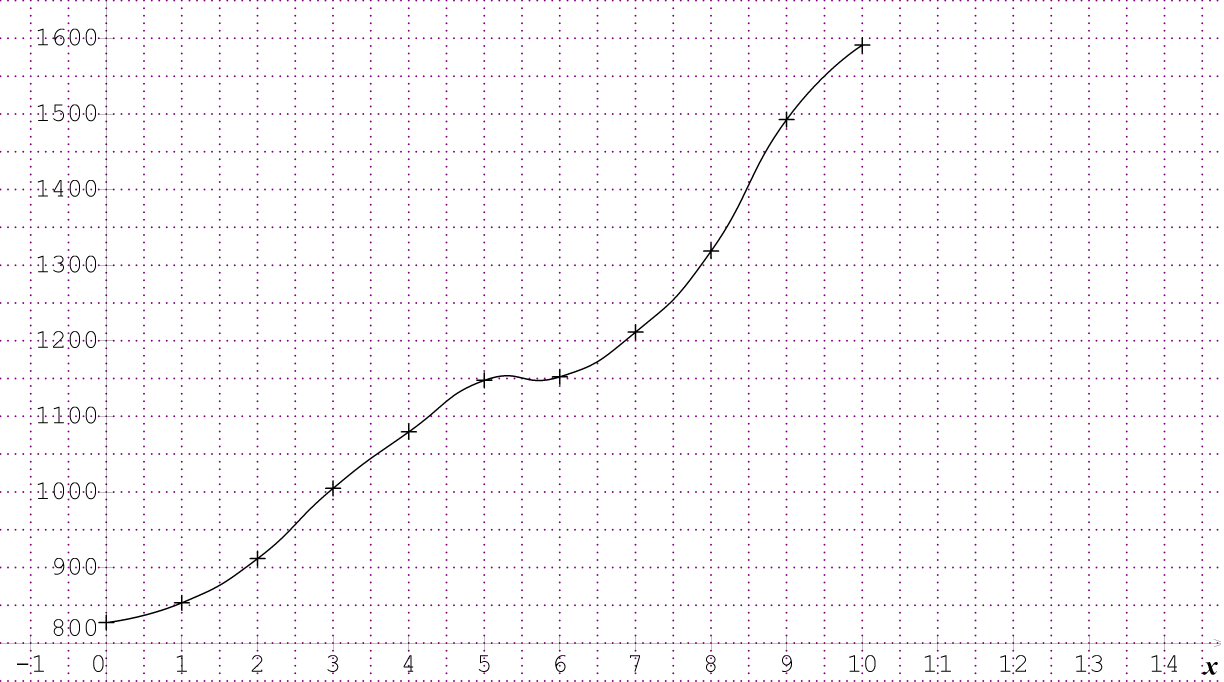
on ne vous a pas demandé de relier les points ce qui n'aurait aucun sens
une approximation affine est envisageable car les points semblent se regrouper dans une même direction
Oui les points ce sont reliés car je ne m'y connait pas trop en logiciel informatique, je sait qu'il ne faut pas les reliés
Pour la question 2 c) J'ai fait ce calcul là : (0+1+2+3+4+5+6+7+8+9+10)/11=5
(827,3+853,3+912+1004,9+1079,5+1147,6+1152,2+1211,6+1318,6+1492,7+1591,2)/11=1144,6
G a pour coordonnées (5;1144,6)
Est ce juste ?
Pour tracer la droite vous avez déjà un point il vous en faut un deuxième
Àpartir de ce point, si vous vous déplacez d'une unité il faudra monter de 76.4 unités soit 0.764 cm
si vous vous déplacez de 2 monter de
etc
Donc si j'ai bien compris, le premier point est le point G (5;1144,6)
Mais pour le deuxieme point je n'ai vraiment pas compris désolé.
Merci
Ah d'accord merci !!
La suite de la question d) : l'équation réduite est 76,4x+762,6 c'est bien ça ?
Mais je ne sais pas comment il l'a trouvé c'est un ami qui me l'a donné
si c'est l'équation de la droite précédente vous avez le coefficient directeur et un point
équation de la forme et vous déterminez p en écrivant que la droite passe parle point moyen
si c'est la droite de régression par la méthode des moindres carrés cela se fait à la calculatrice
et vous avez la réponse sur le graphique précédent précisez votre modèle
en revanche je ne vois pas d'où sort le 76,4
Bonjour,
Je n'ai pas compris comment trouver l'équation et la méthode des moindres carrés je ne l'ai pas vue en cour n'y a til pas une autre méthode ?
L'équation d'une droite non parallèle à l'axe des ordonnées est .
On vous donne 76,4 reste à déterminer
sachant que G y appartient
donc d'où
Quant à la méthode des moindres carrés elle est obtenue par la calculatrice.
Il n'y a pas souvent de cours là-dessus au mieux une brève explication
2 d
Il n'y a pas de problème c'est l'équation de la droite passant par G de coefficient directeur 76.4 donc
Question 3 j'utiliserais le calcul fait par la machine
a=73,5 et b= 777,2
3 b Prendre cette équation pour l'estimation en 2014 et aller chercher le montant du déficit en 2014 pour comparer
Non cette équation est la réponse à la question 2 d
Savez-vous calculer l'équation de la droite de régression avec la calculatrice ?
liste 1 les liste 2 les
et calcul
Ce n'est pas une équation et d'où vient-elle ?
Usage de la calculatrice ou de sine qua non il n'y a qu'à relever le résultat
Euh je suis désolé mais je ne comprend pas avec ma calculatrice jai mit les x dans liste 1 et les y dans liste 2. Ensuite j'ai fait Reglin (ax + b).
Je me suis tromper svp après avoir mit les liste que doit je faire ?
La première chose aurait été de préciser de quelle calculatrice vous avez l'usage.
Je présume une casio dans calcul set (F6) qu'avez- vous ?
moi non plus il faudrait savoir ce que vous avez tapé
Avez - vous fait le ménage avant ? clear L1,L2 ?
vous pouvez comparer avec sine qua non
Paramètres X Y
Moyenne : 5 1144,63
Écart type : 3,16228 237,19
Premier décile : 1 853,3
Premier quartile : 2 912
Médiane : 5 1147,6
Troisième quartile : 8 1318,6
Neuvème décile : 9 1492,7
Calculs
Covariance : 734,818
Coefficient de corrélation linéaire : 0,979679
Coefficient de corrélation : 0,979679
Nature de la régression : Linéaire
Équation de la courbe de régression : y = 73,48181818 x + 777,2181818
Je suis allé dans STATS --> EDIT j'ai éditer les lister (L1 et L2)
Ensuite je suis allée dans CALC --> Reglin (ax + b)
Voila ce que j'ai fait