Annuler
connectez vous
- Un Cours sur les ensembles mathématiques - seconde
- Cours sur les nombres, les ensembles et les nombres premiers - seconde
- Rappel sur les nombres premiers suivi de neuf Exercices d'application - seconde
- Cours sur les valeurs absolues, les encadrements, les distances - seconde
- Petit Exercice d'initiation aux valeurs absolues - seconde
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. SecondeForum de Maths Seconde Nombres et calculs, valeurs absoluesTopics traitant de Nombres et calculs, valeurs absolues [tout]Lister tous les topics de mathématiques
Niveau seconde
Sudomath
Posté par titi56fun
Bonjour , j'ai actuellement fait 23 questions mais je bloque sur 5 questions les voici :
1)Partie entiére de l'antécedent de 6/25 par la fonction inverse.
2)valeux de x solution de { -x - 2y = 0
{ 5x + 7y = 9
3) Plus grand entier de ] -oo ; 16/7 ]
4) ?V32 + 4V72 = 36V2
5) Dans la division de 54 par ce nombre, le quotient est égal au diviseur
Bonjour,
Pour la 1) on te demande de trouver la partie entière de l'antécédent de 6/25 par la fonction inverse
Il faut donc commencer par trouver l'antécédent de 6/25 par la fonction inverse ... As-tu une petite idée de la réponse ?
Si tu as du mal et que tu veuilles commencer par plus simple, que répondrais-tu si on te demandait
l'antécédent de 1/2 par la fonction inverse
l'antécédent de 1/10 par la fonction inverse
alor : A6: Nombre maximum d'angles obtus dans un triangle : 1
A8: Cube du seul nombre premier pair : 8
A9: NUmérateur de la fraction irreductible égale à 16/280 : 2
B2: Nombre de solution de l'équation x² - 9 = 0 : 2
B5: 25 pourcent de 16 : 4
B8: Nombre de chiffres pairs dans le systéme décimal : 5
C1: image de V3 par la fonction carrée : 3
C4: Nombres de merveilles du monde : 7
D1: Nombre de solides de platon : 5
D6: Numérateur de la fraction irréductible égale à 3/40 x 24/7 : 9
D7: Chiffre des dizaine de 0,43/0,001 : 8
D9: Nombre d'arêtes d'un tétraèdre :6
E3: Nombre de faces d'une pyramide à base hexagonale : 6
E5: Coefficient directeur de la droite passant par A(2;10) et B(O ; -2) : 2
E7: plus petit entier strictement positif solution de (8-x)(4x+9)<64 - x² : 8
F3: Nombre de médiatrices dans un triangle : 3
F9: Seul nombre non nul à être ni premier ni composé : 1
G6: Nombres de faces planes d'un cylindre : 2
G7: Reste dans la division euclidienne de 46 par 3 : 1
G9: Nombre de faces d'un prisme à base pentagonale : 7
H5: Nombre de lettres du mot SUDOMATHS : 9
H8: Nombre de multiples de 43 compris entre 0 et 220 : 4
I2: V2°
I4: Nombre maximum de dimanches au mois de février : 5
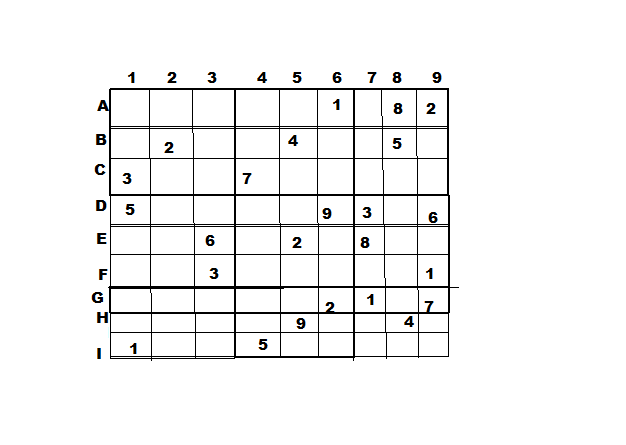
Voila se que j'ai fait , cela ma permis de completer le sudoku. les question 1,2,3,4,5 correspondent a: C3,F1,F4,H2 et I2
Soit r un nombre. Sa partie entière est l'entier n tel que
1°) (n est inférieur ou égal à r)
2°) C'est le plus grand possible : n+1 n'est plus inférieur ou égal à r. On a r< n+1
Autrement dit, la partie entière de r est l'entier n qui vérifie n\leq r< n+1.
Exemple : la partie entière de est 1 car
.
Quelle est la partie entière de ? Quelle est la partie entière de 25/6 ? Quelle est la partie entière de 10 ?
merci 
pour la question il faut faire une équation donc je vais essayer la deuxieme qui ma l'air plus facile : 5x + 7y = 9
5x + 7(0-x)= 9
La première équation te permet d'exprimer y en fonction de x : y = ?
Tu remplaces y par cette expression en fonction de x dans la deuxième équation, et tu as une équation avec une seule inconnue x.
Bonjour Titi56Fun.
Tes réponses à D3, E3 et E5 ne sont pas justes.
Ta réponse à I2 n'est pas dans la bonne case.
Tu as en fait répondu à vingt-quatre questions.
Quelles sont les cases correspondant aux questions qui te posent problème ? Car ne te demande-t-on pas aussi de résoudre le "sudoku" ?
oui , alors pour E3 c'est 7 et pour E5 c'est 1 merci de m'avoir prévenue . en faite il ne me manque plus que 4 question pour réussir et aprer il faut que je résoud se sudoku.
D7 : 430 millièmes divisé par 1 millième = 430; le chiffre des dizaines est 3
E5 : (-2-10)/(0-2) = -12/-2 = 6
E7 : (8-x)(4x+9) < 64-x²
(8-x)(4x+9) < (8+x)(8-x)
x = 9 : -1*45 < 17*(-1) est vrai
x = 9 : 0 < 0 est faux
0 < x < 8 : on peut diviser les deux membres par le nombre positif 8-x
4x+9 < 8+x et 3x < -1 sont faux
La solution E7 est 9 et non 8.
Ah oui merci beaucoup : j'ai une dernière question
I2: Dans la division de 54 par ce nombre , le quotient est égal au diviseur.
j'ai essayer 54 diviser par 1,2,3,4,5,6,7,8,9 mais le quotient n'est jamais égal au diviseur.
c'est à dire que j'ai essayer 54/1 = 54 , 54/2 = 27 , 54/3= 18 , 54/4 = 13,5 ; 54/5 = 10,8 , 54/6 = 9 , 54/7=54/7 =7,7 ,
54/8 = 6,75 , 54/9 = 6.
Je pense que le quotient qui est égal au diviseur est 7.