Inscription / Connexion Nouveau Sujet
suite
Bonjour :
est ce que vous pouvez m'aider a faire cette exercice s'il vous plait.
Voici l'exercice:
Soit la suite(un) définie par u0=3
un+1=2un-1
1. Calculez les cinq premiers termes de la suite
2. Démontrez par recurrence que 

 , un=2n+1 +1
, un=2n+1 +1
Merci d'avance
salut
et alors ? question 1/ ?
2/ quelle est alors l'hypothèse de récurrence ?
que doit-on vérifier pour faire un raisonnement par récurrence ?
Que donnent les premiers termes ?
ne doivent être entre les balises que les indices, u doit être à l'extérieur
Vous le faites une fois sur deux presque
1. u0=3
un+1=2un-1
u1= 2*u0-1=5
u2= 2*u1-1=2*5-1=9
u3= 2*u2-1=2*9-1=17
u4= 2*u3-1=2*17-1=33
u5=2*u4-1=2*33-1=65
c'est ça ?
2. Je ne sais pas
De 0 à 5 cela fait 6 termes donc les 5 premiers s'arrêtent à
comme d'habitude
et calculez
en tenant compte de la relation de récurrence et de la définition de la suite
Oui, les calculs sont corrects 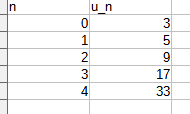
ensuite non vous avez mélangé indice et exposant
hypothèse
calcul à effectuer
ca c'était l'hérédité ducout ? et l'initialisation ? et pour la conclusion il faut mettre que la proposition un+1 est initialisée pour n=0 et est héréditaire donc elle est vraie pour tout naturel n c'est ça ?
Initialisation 13 :39
oui, 15 : 59, c'est bien pour l'hérédité
n'est pas une proposition, c'est un terme de la suite
Soit p(n) la proposition p(n) :
elle est vraie pour et
entraîne
elle est donc vraie pour tout
ducout non du coup
Bonjour :
excusez moi je suis entrain de recopier et pour l'exercice 3 je n'ai pas bien compris pour la question 2 est ce que vous pouvez regarder si c'est bien ça ?
Initialisation :
n=0 u0=3 u0 0
0
hérédité :
Supposons jusqu'à l'entier naturel k uk 2k+1+1 et montrons que uk+1
2k+1+1 et montrons que uk+1 2k+2+1
2k+2+1
uk 2k+1+1
2k+1+1
uk+1 2uk-1
2uk-1
uk+1 2*(2k+1+1) -1
2*(2k+1+1) -1
uk+1 2k+2+2-1
2k+2+2-1
uk+1 2k+2+1
2k+2+1
C'est juste ou il faut mettre un = a la place de 
Supposons qu'il existe un réel tel que
et montrons que
Confusion entre exposant et indice on a = pas une inégalité
définition de la suite
remplacement de
en tenant compte de l'hypothèse de récurrence
Développement de la parenthèse et simplification
On retrouve bien la valeur de en utilisant la relation de récurrence
J'ai réécrit, car il était plus facile d'utiliser pour écrire les égalités
Non pour initialisation il faut évidemment utiliser la relation
pour
La relation est bien vraie
du coup, beaucoup cela doit être un coût pour vous d'écrire coup


