Bonjour,

En seconde, t'étudies que des termes de la forme ax+b.

ax+b=0 lorsque x=-b/a (valeur à mettre dans le tableau de signes).

Concernant le signe, ax+b>0 si, et seulement si, ax>-b.

Deux cas se présentent : a>0 ou a<0.

Si a>0, alors ax>-b si, et seulement si, x>-b/a.

Si a<0, alors ax>-b si, et seulement si, x<-b/a (on divise par un nombre négatif donc l'inégalité change de sens).

Conclusion : à gauche de la valeur d'annulation (x=-b/a) on met le signe de (-a) et à droite on met le signe de (+a).

Prenons un exemple :

Étudier le signe de f(x)=x^2-1.

f(x)=(x-1)(x+1)

f(x) s'annule pour x=-1 et x=1, ce sont donc les valeurs à placer dans le tableau de signes.

  x    -00     -1     1    +00

x-1                  0

x+1            0

f(x)            0     0


Or x-1>0 si, et seulement si, x>1.

Et x+1>0 si, et seulement si, x>-1.

D'où :

  x    -00     -1     1    +00

x-1        -      -  0   +

x+1        -   0  +      +

f(x)        +   0  -  0   +

Merci de ta réponse tout d'abord, puis, si je comprends bien, lorsque x est plus grand que l'expression, on met "+" à droite, alors que lorsqu'il est plus petit que l'expression, on met"-" à gauche?

Bonjour,

Tes facteurs seront souvent du type ax+b.

Exemple :
3x+2

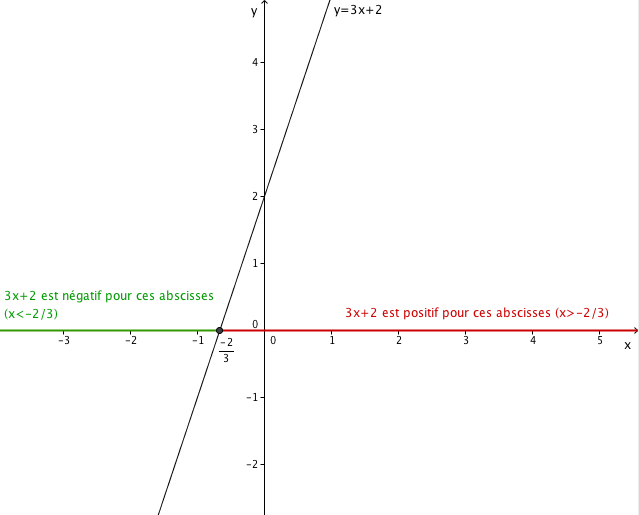
1) ça s'annule en x=-2/3 (graphiquement : la droite d'équation y=3x+2 coupe l'axe des abscisses au point (-2/3,0))

2) C'est négatif pour x ≤ -2/3, positif pour x ≥ -2/3
Pour le voir, suffit d'imaginer la fonction correspondante ! 3 est positif donc la droite y=3x+2 "monte", donc dans le tableau ça va être des - d'abord (jusqu'à x=-2/3) puis des +



Pour le prouver tu peux toujours résoudre :
3x+2 > 0
ssi 3x > -2
ssi x > -2/3
donc 3x+2 est positif pour x>-2/3 --> on met des + à partir de x=-2/3
(et du coup, 3x+2 est négatif ailleurs, donc des - avant -2/3)

Pour résumer : si c'est un facteur du type ax+b, il suffit de savoir si la fonction est croissante (cas où a est positif) : alors ce sera des - puis des +) ; ou décroissante (cas où a est négatif ; dans ce cas ça sera d'abord des + puis des -).

----------------------------
Tu pourras aussi avoir des facteurs du type (qqch)² : ceux-là sont positifs partout (un carré est toujours positif).
Bien entendu, du coup -(qqch)² est toujours négatif.

  Merci pour vos réponses à tous les deux, elles sont très explicite.
  Si je comprends bien :

ax+b > 0  ; pour a > 0 cela donne "-" puis "+" , et pour a < 0 cela donne "-" puis "+"?

ax+b < 0  ; pour a > 0 cela donne "+" puis "-" , et pour a < 0 cela donne "-" puis "+"?

Non... Pour rester dans ta démarche, j'écrirais plutôt :

Si on a un terme de la forme ax+b alors, pour a > 0 cela donne "-" puis "+" , et pour a < 0 cela donne "-" puis "+".

(tes phrases avec les inégalités n'ont pas de sens...)

D'ailleurs, il y a une petite erreur :

Si on a un terme de la forme ax+b alors, pour a > 0 cela donne "-" puis "+" , et pour a < 0 cela donne "+" puis "-".

Daccord, je pense avoir compris ces tableaux de signe, donc un grand merci à vous deux.

Voilà un tableau qui récapitule ce que l'on vient de te dire :

Après tu as des exemples plus complexes résolus ici :

Quand il s'agit d'une fraction, on met une double-barre dans le tableau pour signaler les valeurs interdites.



Bonjour masterrr

Bien le bonjour critou