Bonjour,

tu sais qu'une quantité peut être positive, négative ou nulle ?
tu connais le produit nul ?
tu connais la règle des signes ?

bsr,

pour quelle valeur de x a-t-on 2x-1=0 ?
pour quelle valeur de x a-t-on 5-2x=0 ?

@Barney

tu sais qu'une quantité peut être positive, négative ou nulle ? Non
tu connais le produit nul ? Non
tu connais la règle des signes ? Oui


@Bouli1407

pour quelle valeur de x a-t-on 2x-1=0 ?  2x-1 = 0 <=> x = -1/2
et
pour quelle valeur de x a-t-on 5-2x=0 ? 5-2x = 0 <=> x = -2/5

est-ce bien ça ?

heu...

2*(-1/2)-1 = -2   et   5 - 2*(-2/5)= 29/5

Oh merci !

Ensuite je fais le tableau...mais comment placer les signes ? Et les O

Je réitère ma question :

pour quelle valeur de x a-t-on 2x-1=0 ?
pour quelle valeur de x a-t-on 5-2x=0 ?

pour quelle valeur de x a-t-on 2x-1=0 ? -2x+1 ?

Je suis désolé, je ne comprend pas du tout

2x-1=0 donc x=.....   (x n'est pas égal à -1/2)

2x-1=0 donc x= -2

remplace x par -2 dans 2x-1 et tu verras que tu n'obtiens pas 0
donc x n'est pas égal à -2

Pouvez-vous donner la réponse pour cette question :
pour quelle valeur de x a-t-on 2x-1=0 ?  

puis j'essayerai de faire la deuxième car je suis extrêmement perdu là !

heu....  c'est du niveau 4e quand même...

2x-1=0
2x=1
x=1/2

4ème...J'ai honte
Est-ce bien de l'équation ce genre d'exercice ?
J'aimerai revoir mes bases...

équation du 1er degré !

ensuite : 5-2x=0  donc 5=2x  donc x=5/2

On connait donc maintenant les valeurs pour lesquelles 2x-1 et 5-2x s'annulent

donc on connait les valeurs pour lesquelles le produit (2x-1)(5-2x) s'annule

Ton tableau de signe devrait donc commencer à ressembler à ça :



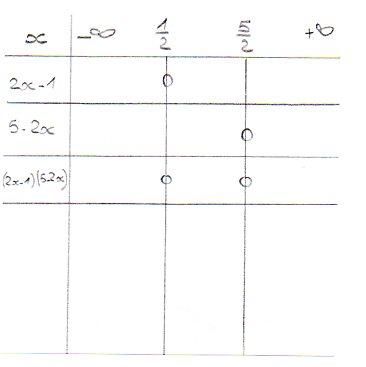
Ensuite : quel sera le signe de 2x-1 si x est compris entre - et 1/2  ?
          quel sera le signe de 2x-1 si x est compris entre 1/2 et 5/2  ?
          quel sera le signe de 2x-1 si x est compris entre 5/2 et +

pareil pour 5-2x

on en déduit le signe du produit (2x-1)(5-2x)

etc...etc...

Voilà, j'ai essayé de faire les deux premiers.

Donc, pour toi, si, par exemple, x=0, alors 5-2x est négatif ?

            et, si, par exemple, x=1 ou 2, alors 5-2x est négatif ?
  
            et, si, par exemple, x=3, alors 5-2x est positif ?


heu.....   je ne suis pas d'accord

Je vois ce que tu as fait :

comme dans la ligne 2x-1, tu as trouvé :
    négatif  jusqu'à la valeur qui annule 2x-1, puis positif

alors, dans la ligne 5-2x, tu as recopié : négatif jusqu'à la valeur qui annule 5-2x, puis positif

ça aurait été effectivement le cas si on avait eu 2x-5, mais ici on a 5-2x

J'ai enfaite regardé un exercice fait en classe qui était pour moi similaire à celui là...J'ai donc essayé de le reproduire

"quel sera le signe de 2x-1 si x est compris entre - et 1/2  ?
quel sera le signe de 2x-1 si x est compris entre 1/2 et 5/2  ?
quel sera le signe de 2x-1 si x est compris entre 5/2 et + "

Comment puis je trouver le signe ? Quelles sont les étapes à faire ?

Si x=0  alors 5-2x = 5-2(0) = 5-0 = 5  (positif)

si x=1  alors 5-2x = 5-2(1) = 5-2 = 3   (positif)
si x=2  alors 5-2x = 5-2(2) = 5-4 = 1   (positif)

si x=3  alors 5-2x = 5-2(3) = 5-6 = -1  (négatif)


on a donc :



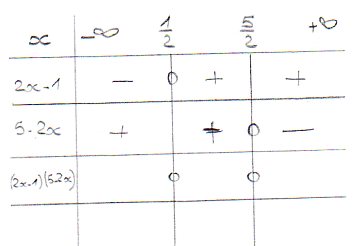
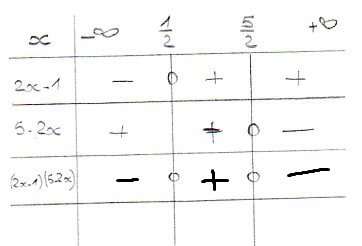
Ensuite, tu as répondu OUI quand Barney t'a demandé si tu connaissais la règle des signes.
Donc, tu peux remplir la ligne (2x-1)(5-2x)

Voilà...J'espère que j'aurai au moins eu bon a celui là

Oublié d'attaché l'image !

Oh non encore oublié

Voilà, on y est !

Tu as donc, sous les yeux, l'ensemble des solutions de l'inéquation (2x-1)(5-2x) < 0

Wahouu ! Merci beaucoup Bouli1407 et merci d'avoir été patient.

Je t'en prie.
J'espère juste qu'après ça, tu seras capable de refaire un exercice de ce type.

Peux-tu juste écrire la phrase de conclusion de cet exercice ?

Donc s =  [ -oo;1/2 [U] 5/2 +oo ]

J'ai regardé dans tout mon cahier et...c'est très très aléatoire ce que je viens de dire

Ok !

Juste un petit détail : les crochets à gauche -  et à droite de +  doivent être tournés dans l'autre sens

s =  ]-;1/2 [U] 5/2 +[

Toujours dans l'autre sens ?

toujours !

par définition est infini...

D'accord ! Et concernant l'intersection le U et le U a l'envers, comment cela marche ?

tout est là : http://www.educastream.com/intervalles-seconde

Pour faire plus simple, on pourrait dire : U comme union (union de 2 intervalles)

Dans ton exercice, l'ensemble des solutions est constitué de l'union de deux intervalles :

  ]-;1/2[    et    ]5/2;+[

donc s =  ]-;1/2 [U] 5/2 +[

D'accooord ! Merci beaucoup