Bonsoir,

donc
g(x) est positif quand x est inférieur à -0,5

Bonsoir,

Une fonction est toujours de la forme :

f(x) = ax + b.
Bon, là ta fonction s'appelle g donc ce sera g(x) = ax + b.
a c'est le coefficient directeur et b l'ordonnée à l'origine.
Si a est positif, alors la fonction est croissante et donc le tableau de signe commencera par - et après +.
Si a est négatif, c'est l'inverse, le tableau de signe commencera par + et après -.

Ici, tu as g(x) = x + 0,5 : Donc a = 1 et b = 0,5.
a est positif donc ta fonction est croissante, donc c'est d'abord - et ensuite + dans ton tableau de signe

Et pour savoir à quel moment tu changes de signe, tu dois résoudre g(x) = 0.
Autrement dit, résoudre x + 0,5 = 0 soit x = -0,5, tu étais sur la bonne voie

Du coup ton tableau de signe devrait ressembler à :

x          -        -0,5        
g(x)        -            0            +

tu as sûrement voulu écrire "g(x) est positif quand x est supérieur à -0,5" ?

rectification....
g(x) est positif quand x est supérieur à -0,5

Donc du coup j'ai juste a mettre g(x) = x+0,5>0
                                        x > -0,5
Et que g(x) et positif quand x est inférieur à -0,5

Donc pour le tableau de signe sa va donner quoi ?

Cordialement
                                        

D'accord merci beaucoup

....lis mon rectificatif

Oui je viens tout juste de voir les autres reponses

il y a un bon truc pour ne pas se tromper avec les tableaux de signes des fonction affines.

y = ax + b, si a > 0 est monte sinon si a < 0 elle descend.
si elle monte le tableau de signes sera - + et si elle descend, ça sera + -

Merci beaucoup pour votre conseil je le retiens

Par contre j'ai encore une question
Enfainte il y'a encore des questions sur cette activité
Donc il faut que je reface un topic pour poser une nouvelle question ou je peux la poser sur celui la ?

Merci

sur celui là.

OK donc du coup
quels et le signe de f(x) pour x > 1,5
Quels et le signe de g(x) pour x > 1,5

Sachant que f(x) = -2x+3
            g(x) = x+0,5

                

f(x) est décroissante puisque son coefficient directeur est négatif.
Lorsque x = 1,5, f(x) = 0.
f(x) est décroissante comme on le disait, donc dans le tableau de signe, f(x) est positive lorsque x < 1,5 et négative lorsque x > 1,5
Fais pareil pour g(x)

Merci donc du coup le tableau de signe va d'abord commencer avec le + puis après le - c'est sa ?

Est je fais le g(x) puis ensuite je vous le montre

Cordialement

Oui c'est ça
Oui vas-y tu montreras quand tu auras fini, bien sûr

Donc du coup pour g(x)

g(x) est croissante puisque le coefficient directeur est positif
Lorsque x = 1,5      g(x) = 1

Donc le tableau de signe commence d'abord par le - et après le + c'est sa ?

Cordialement

Si g(x) = x + 0,5, alors si x = 1,5, g(x) ne vaut pas 1 mais 2 !
g(1,5) = 1,5 + 0,5 = 2, comment as-tu trouvé 1 ? ^^

Enfin bref, puisque le coefficient directeur est positif comme tu le disais, g est croissante.
Vu que pour x = 1,5, g(x) > 0,
Alors pour x > 1,5, g(x) > 0 !
Et oui tu as raison pour le tableau de signe

Merci beaucoup
Est ces que je peux encore vous posez une question de mon activité ?

Cordialement

Bien sûr, tu n'as pas à demander ^^
Bon par contre la prochaine fois pose tout d'un coup dès le début

D'accors merci beaucoup de votre patience

Alors voilà

1) quel est le signe de f(x) × g(x) lorsque x est strictement supérieur à 1,5
f(x) = -2x+3
g(x) = x+0,5

2) Quel est le signe de f(x) pour x strictement supérieur à 0,5 puis quand x appartient à l'intervalle ]-0,5;1,5[  

3) quel est le signe de f(x) × g(x) lorsque x strictement supérieur à 0,5 puis quand x appartient à l'intervalle ]-0,5;1,5[  

Merci cordialement

Et bien la 1) est faite du coup,
Pour la 2), f(x) = 0 lorsque x = 0,5.
Puisque f est décroissante, lorsque x > 0,5, f est donc négative.
Pour quand x appartient à l'intervalle ]-0,5 ; 1,5[, fais un tableau de signe puisque f change de signe lorsque x = 0,5.
Suis le même raisonnement pour la 3)

Pourquoi la 1 est faite ?

Pardon pour la question 2 et 3 c'est strictement inférieur à -0,5 et non pas supérieur à 0,5

Cordialement

Ben, la 1) on y a répondu quelques messages plus haut, relis...
Que ce soit inférieur ou supérieur n'y change pas grand-chose : puisque f(1,5) = 0 et que f est décroissante,
Alors comme je l'avais dit plus haut, f est positive pour x < 1,5 et négative pour x > 1,5 !
Si f est positive pour x < 1,5, alors f est forcément positive pour x < -0,5...
Du coup, quand x appartient à l'intervalle [-0,5; 1,5[, f est positive.

3) Tu vas devoir faire un tableau de signes à 3 lignes, la première ligne ce sera -2x+3, la deuxième ligne ce sera x+0,5, et la dernière ligne ce sera f(x) * g(x), et ça te donnera le signe de f(x) * g(x)
Un exemple similaire :

Mais dans la 1 il faut multiplier
On a jamais multiplié dans 'es message plus haut

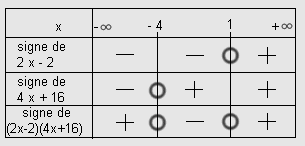
Ah oui excuse-moi je n'avais pas vu la formulation légèrement différente !
Bon, et bien en tous cas quelques messages plus haut on avait trouvé que f était négative lorsque x > 1,5, tu es d'accord avec moi ?
g(x) = x + 0,5 donc g(1,5) = 2 et g est croissante donc pour x > 1,5, g(x) > 2 donc positive, toujours d'accord ?
Donc pour x > 1,5, on a f négative et g positive... Si on multiplie les deux entre elles, on a du négatif, parce que plus par moins ça fait moins, et voilà le travail !

Est enfaite pour le tableau c'est la question d'apres on me le donne avec les 3 lignes que vous m'avait dit j'ai juste a la complèter avec les signes et les 2 x

Donc pour la question 3 je dois faire un calcul je pense

Cordialement

Si on te donne le tableau pré-complété pour la question 3 alors tu n'as pas à faire de calcul, juste à lire le tableau pour répondre à a question... ?

Si tu dois trouver le signe de f(x) * g(x) lorsque x < -0,5, c'est exactement le même raisonnement que trouver le signe de f(x) * g(x) lorsque x > 1,5... Et ça tombe bien, ça je l'ai écrit juste au-dessus de ton message

Bâ enfaite on me demande de trouver le signe et ensuite de compléter le tableau

Ok, ben vas-y go !