Inscription / Connexion Nouveau Sujet
Tableau de variation
Bonjour, j'aimerais savoir si mon tableau de variation pour e-0,05t=2/7 est bon.
J'ai trouvé qu'elle admet une solution=25,07
et aie du coup construit ce tableau
| t | 0 25 +oo |
| e-0,05t | 0
2/7 +oo |
Bonsoir
Quel est le texte exact ?
Vous donnez une équation et vous parlez de tableau de variation c'est vraiment peu clair
Bonjour,
Mets à jour ton profil s'il te plait. Tu n'es plus en première.
+ en bas d'un tableau, et 2/7 sous 0, ça ne te fait pas tiquer ?
en bas d'un tableau, et 2/7 sous 0, ça ne te fait pas tiquer ?
Et si tu recopiais l'énoncé ?
Ça éviterait de parler des variations d'une équation ; ce qui n'a pas de sens.
C?est fait..
1. On cherche à quel moment les proportions a(t)=0,3+0,7e-0.05t de produit A sont égales au proportion b(t)=0,7-0,7e-0.05t de produit B
a(t)=b(t)
0,3+0,7e-0,05t = 0,7-0,7e-0.05t
2. Justifier que cet équation équivaut à e-0,05t=2/7
J?ai réussi à prouver cette partie
3. Completer le tableaude variation ci-contre (image) et justifier que l?équation e-0,05t=2/7 n?a qu?une solution j?ai réussi à prouver ici aussi avec t=25,07s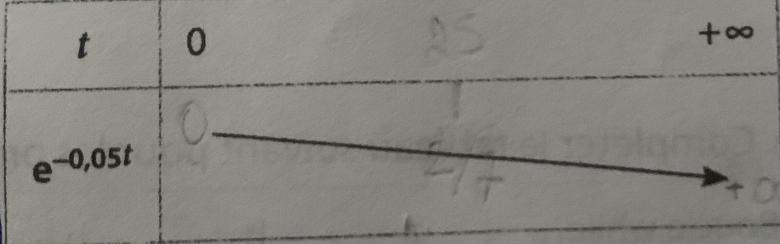
***Modération : tableau redressé (2ème fois), la prochaine fois essaie de mettre les images dans le bon sens***
Bonjour,
Inutile de faire une limite en 0.
Poser f(t) = e-0,05t et calculer f(0).
Noter a la solution de l'équation, après avoir justifié son existence et unicité.
Dans le tableau, ne pas écrire une valeur approchée de a, mais la lettre a.
Bonjour Sylvieg
Oui on peut faire plus simple que de chercher la limite.
Je n'appellerai pas la solution, car
est déjà le nom d'une des fonctions.
Bonne journée
Effectivement, la lettre a n'est pas adaptée 
Je disparais pour la journée.
Bonne continuation à tous les deux.
Ah j'ai compris!
Du coup pour t=0 on a e-0,05t= 1
t=+oo on a e-0,05t=0 (d'où la flèche qui décroît..)
Est-ce qu'il faut que je rajoute le Bêta sous Alpha?
En tout cas merci de votre aide et bonne journée.

 c'est mieux, mais plus compliqué à écrire.
c'est mieux, mais plus compliqué à écrire.
