Inscription / Connexion Nouveau Sujet
Tangentes de points parrallèles à une asymptote.
Bonjour à tous, voici mon soucis :
Soit la fonction f(x)=(x^3+2x²)/(x²-1).
Elle admet une asymptote oblique en -/+ l'infini d'équation y=x+2
1) Déterminer l'abscisse des points de la courbe C de f, ou la tangente est parallèle à la droite d'équations y=x+2.
Je ne vois pas comment faire, il faut quelles aient un coeffficient directeur de 1 mais je ne vois pas comment trouver leurs équations et points d'abscisses .
Merci d'avance à vous !
Bonjour 
Le coefficient directeur d'une tangente à une courbe en un point a vaut f'(a)
Ici comme tu l'as dit, le coefficient directeur vaut 1 donc il faut que tu cherches les x tels que f'(x)=1
Bonjour à tous, j'ai encore un petit soucis :
Soit f(x)=(x^3-2x²)/(x²-1).
Dérivée : f'(x)=(x^4-3x²-4x)/(x²-1)²
Nous savons que y=x+2 est asymptote oblique à f.
1) Déterminer l'abscisses des points de la courbe de f, ou la tangente est parallèle a cette asymptote oblique.
J'ai donc poser f'(x)=1 équivaut à x^4-3x²-4x=(x²-1)²
-x²-4x+1=0
Delta=20, donc il y a deux racines : X1=(4- 20)/-2 et X2=(4+
20)/-2 et X2=(4+ 20)/-2.
20)/-2.
Ces deux racines seraient donc les points d'abscisses ou la tangentes est parallèele à l'asymptote oblique. Pourrais je avoir une confirmation ?
*** message déplacé ***
Bonjour,
J' ai pour la dérivée:
(une erreur de signe).
l' équation donne ensuite:
qui donne les racines 2

*** message déplacé ***
Bonjour, oui la dérivée vaut (x(x3-3x+4))/(x2-1)2 mais pour f'(x)=1 moi j'ai trouvé 2
 3
3
*** message déplacé ***
Bonjour cailloux,
Par acquis de conscience, je venais de vérifier aussi.
Merci de m'avoir évité de devoir le taper 
*** message déplacé ***
Au fait:
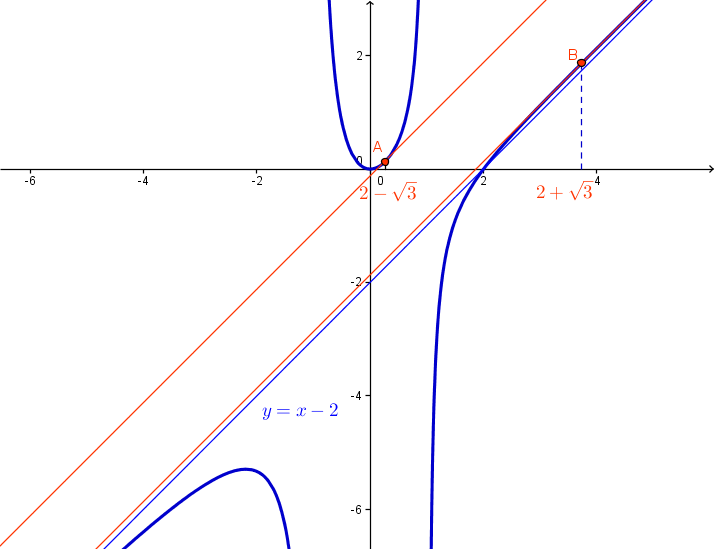
Nous savons que y=x+2 est asymptote oblique à f.
Plutôt

*** message déplacé ***
De plus, je n'ai aucun soucis dans le signe de ma dérivée, c'est bien f'(x)=(x^4-3x²-4x)/(x²-1)² !
*** message déplacé ***
Oh, moi, je n' ai rien à prouver; je te dis simplement que tu t' es trompé... 
*** message déplacé ***
Mais c'est qu'il mordrait ! 
Du calme. Ca arrive à tout le monde de passer à côté d'une erreur de signe, même aux plus chevronnés.
Cailloux a raison. J'ai moi aussi trouvé le même résultat. Nous ne sommes pas infaillibles mais sur ce coup, je pense que c'est bon.
*** message déplacé ***
je te le décris montre moi ou je me trompe :
f'(x)=((3x²+4x)(x²-1))-((2x)(x^3+2x²)/(x²-1)²
=(3x^4-3x²+4x^3-4x)-(2x^4+4x^3)/(x²-1)²
=(3x^4-3x²+4x^3-4x-2x^4-4x^3)/(x²-1)²
=(x^4-3x²-4x)/(x²-1)²
*** message déplacé ***
Equinoxe, regarde plus haut, je te l'avais donnée la dérivée, cailloux aussi. c'est +4x et pas -4x
*** message déplacé ***




