Bon.

En topo, on parle de gisement :
ce sont des angles orientés dans le sens horaire,
c'est à dire dans dans le sens inverse  du sens trigo,
avec une origine suivant l'axe Oy (Nord).
L'unité d'angle est le grade (100 grades = 90° = pi/2)

Pour la passage de polaires à rectangulaires ,
les formules sont inverses à celles utilisées en trigo
à cause justement du système de référence angulaire :

dx = d * sin (G)
dy = d * cos(G)

bonjour,
je rencontre des soucis avec cette exercice de topographie de base,
alors on me demande tout simplement de calculer les cotes périmétriques, et les angles intérieur, " ce que j'ai en partie réussie à faire avec multiples calcules, il faut aussi calculer les gisements s1d, s1c, s2a et s2b, mais la ou je bloque le plus c'est quand on me demande les coordonnées rectangulaire des quatre points a, b ,c et d, j'ai impression de patauger la..
est ce que A est négatif ou positif par rapport à y?
et comment trouver delta x et y. je suis un peu perdu.
merci d'avance pour votre aide



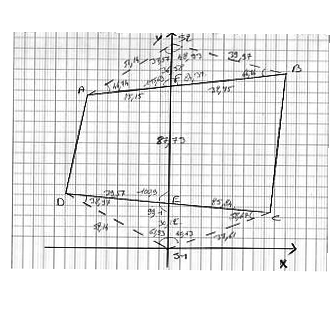
malou > j'ai essayé d'améliorer l'image mais bon...

*** message déplacé ***

excusez moi, c'est involontaire, j'ai bidouillé pour mettre une image qui répond aux exigences
merci pour la correction,
sinon je ne comprend pas bien comment dans le cas présent on peut trouver les distances x et y

Je pense que la personne qui cherchera à vous aider aura besoin d'un dessin un peu plus lisible...(un peu plus grand) j'ai essayé d'améliorer les choses, mais avec la 1re image, pas facile d'obtenir mieux....
malou (modérateur)

Bon, on peut le faire pour C à titre d'exemple.

Quelles sont les coordonnées de la Station S1 ?
l'angle (S1y, S1C) ?
la distance réduite S1C ?

bonjour,
alors D s1 E =61.93g
            C s1 E =40.43g
DC devrait faire 65.41m
E s1 = 30.12m

s1 C=37.61m
s1 D= 52.14m

le truc c'est que j'ai réussi a trouver pas mal de mesure mais ce n'ai pas ce que l'on me demande,
C par exemple serai (x+ y+) et D (x- y+)? et comment trouver la distance AD et BC?
cet exercice est un peu à l'envers par rapport à mon cours...

Bonjour,

Avec tes données et en supposant que est à l' origine du repère:









On retombe bien sur:

merci pour l'info,
de cet manière j'ai bien trouvé les distance AD et DC dont je suis certain, mais pour AD et BC j'obtient 70.338 et 58.759 pour BC, ce qui me parait incohérent par rapport à l'approche que je me suis fait de départ qui dit
entre s1 et s2= 154.43 (sujet)
s2 F= 36.58
FE=87.73
Es1= 30.12
y a t'il des précautions, pour prendre en compte la distance entre s1 et s2?

Le problème c'est qu'il faut déjà arriver à deviner ton énoncé !

Une fois que tu as déterminé les coordonnées de D et de C à partir de s1
Une fois que tu as déterminé les coordonnées de A et de B à partir de s2
les distances AD et CB se déterminent à l'aide des coordonnées de A, D et de B,C

Ensuite si les choses te semblent incohérentes, c'est que tu t'es trompé
dans tes résolutions de triangles S1EC, S1ED, S2FA, S2FB.
d'où des distances S1E e S2F qui sont fausses
d'où une distance EF qui l'est aussi.

voici donc les mesures qui m'ont été fournie du départ.
avec en question de trouver les cotes périmétriques et les angles intérieurs ABCD

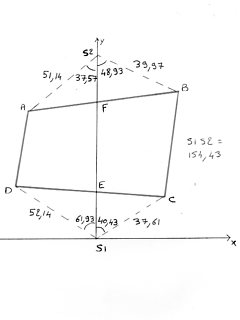
Uniquement avec les résolutions de triangles,
en utilisant la règle des sin et celle des cos :

dans DES1 :

DE = 38.968
ES1 = 29.962
S1D = 52.14

dans ECS1 :

EC = 22.314
CS1 = 37.61
S1E = 29.962

oui, je trouve sensiblement la même chose,
s2f= 36.58
AF= 25.15
FB= 32.75

c'est à dire que s1s2-( s2f+s1e)= EF
soit 154.43- (36.58+29.962)= 87.88
je trouve des distance AD et BC toutes deux plus petite que EF!!!
donc je ne suis pas bon dans mes distances AD et BC.
c'est pour ça que je cherche à comprendre d'où vient mon erreur et j'ai du mal à trouver des explications sur le net.
(faire la liaison entre s1 et s2.)
merci...

En topographie, l' ordre logique des choses ici est de calculer les coordonnées cartésiennes des points comme indiqué à 18h59.

On trouve:

    

              

Ensuite, on a le reste rapidement, par exemple:

  - Pour les distances:

        

  - Pour les angles:

       et (calcul d' un gisement à partir des coordonnées que tu dois connaître)

      

Pour éviter des erreurs d' arrondi, on exprime les distances (et les coordonnées) arrondies au millimètre et les angles au décimilligrade dans les calculs intermédiaires pour obtenir des résultats finaux arrondis au centimètre pour les distances et au centigrade pour les angles.

Pour information, un dessin coté:

  

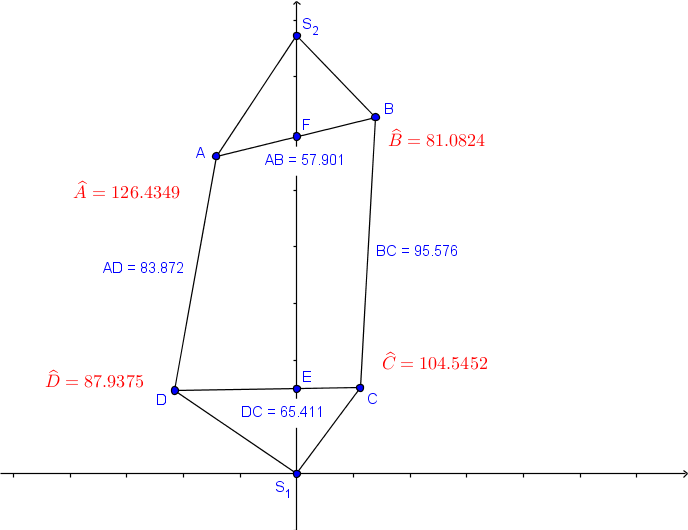
Avec le schéma de Lake, tu as ta réponse :
Les  distances AD et BC toutes deux plus petite que EF !

Comme le dit Lake, les calculs intermédiaires en topo se font au 1/10 ;
le milligrade serait ici suffisant, d'une part, parce que les angles
sont mesures au cgr et que, d'autre part, 1 mgr = 1 mm à 60 m.

j'ai dit une bêtise concernant EF !!
la distances EF est comprise entre AD et BC.

Ah! messages croisés

j'ai tout refait en suivant vos instructions, impec, c'est claire, j'ai bien compris le principe, je vous remercie aussi pour votre aide