Inscription / Connexion Nouveau Sujet
TP tableur
Bonjour voici le sujet
On propose à Pierre le jeu suivant : On lance deux fois de suite un dé parfaitement équilibré. On note
dans l'ordre les nombres x et y de points marqués sur la face supérieure. Pierre gagne s'il y a au plus 3
points d'écart entre x et 2y.
Exemple : Si le premier lancer donne 2 et le deuxième 3, on a x = 2, y = 3 et x - 2y = − 4. L'écart est de 4
points et Pierre a perdu.
Pierre se demande si le jeu est équitable ou non, c'est-à-dire s'il a une chance sur deux de gagner.
b) Faire afficher, pour la simulation effectuée, la fréquence des jeux gagnants puis conjecturer une
réponse à la question posée.
et une aide éventuelle.
2. a) Réaliser un tableau à double entrée ou un arbre représentant les différents cas possibles pour un
seul jeu.
b) Déterminer la probabilité de gagner à ce jeu.
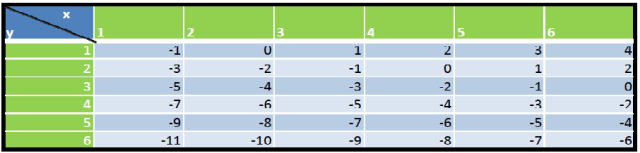
salut, pour gagner il faut que |x-2y| 3 sauf erreur il y a 17 cas favorables et donc
3 sauf erreur il y a 17 cas favorables et donc
P(gagner)= 17/36 , celle de perdre  (perdre)= 19/36
(perdre)= 19/36
Voici un tableau à double entrée
Tu peux vérifier que le nombre de cas favorables est bien 17 sur 36 cas possibles et donc le jeu n'est pas équitable