Inscription / Connexion Nouveau Sujet
Transformation, lieu géométrique, (barycentre)
Tout d'abord bonjour à tous!
J'aurai besoin d'un peu d'aide: Nous avons eu un Devoir Maison en Mathématiques et le problème est que pour le deuxième exercice, je suis complètement bloquée! (Hier soir j'ai cherché pendant plus de 3h sans avoir aucun résultat ni aucune piste)
Voici l'énoncé:
Dans le plan P, on donne quatre points O, A, B et C et un cercle (C) de centre O.
Le point M est un point quelconque variable sur le cercle (C). On associe au point M l'unique point M' du plan P défini par l'égalité:




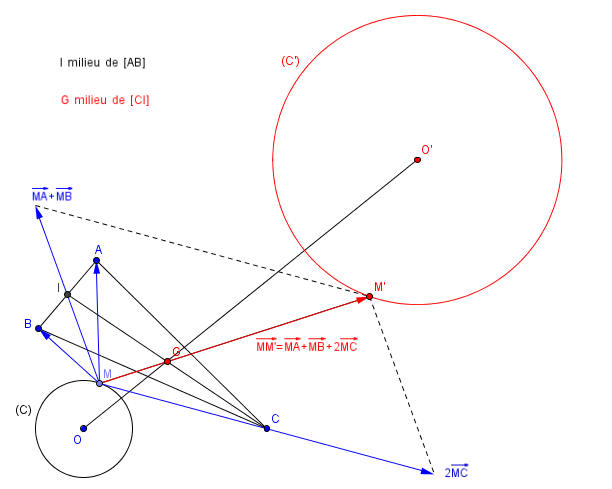
MM'=MA+MB+2MC.
Il s'agit de déterminer le lieu géométrique L du point M' lorsque le lieu géométrique du point M est le cercle (C).
1-a. A l'aide d'un logiciel de géométrie plane construire les points 0, A, B et C, le cercle (C) et le point libre M sur ce cercle.
1-b. Construire le point M' associé à M
1-c. En observant plusieurs positions du point M faire une conjecture sur la nature de la transformation du plan qui transforme M en M', ainsi que la nature du lieu géométrique du point M'.
2-a. Déterminer par le calcul la nature de la transformation du plan qui transforme le point M en le point M'.
2-b. Déterminer le lieu géométrique L du point M'.
Alors moi j'ai le logiciel "Atelier de Géométrie 2D" et déjà j'ai eu du mal à faire la figure et en plus quand je bouge le point M, le point M' ne bouge pas donc je suppose que j'ai pas réussi à la faire et pourtant j'ai essayé plus d'une fois avec toujours le même résultat au final.
Je ne comprend pas la question 1-c. Qu'est-ce que "la nature du lieu géométrique d'un point"?
Et pour l'ensemble de la question 2, je suppose qque l'on va devoir utiliser la notion de barycentre, seulement je ne vois pas du tout ce qu'il faut faire.
Merci!
Personne ne peut m'aider un peu s'il vous plaît?
Bonjour,
Pour le 1c), Considére le barycentre de
est le barycentre de
, c' est à dire le milieu de
C]
et
Soit .
A quoi te fait penser cette transformation ?

Merci de me venir en aide.
C'est une transformation vectorielle?
A un point M elle fait correspondre un point M' tel que
C' est une transformation ponctuelle; elle a un nom bien précis que tu as du voir en 1ère...

C'est une translation qui transforme M en M'
j'espère que c'est ça sinon je ne vois pas.
Par contre je ne comprends pas le terme "lieu géométrique d'un point"
Ah non!, c' est l' homothétie de centre et de rapport -3
Or une homothétie transforme un cercle de centre O et de rayon r en un cercle de centre O' image de O par cette homothétie et de rayon où
est le rapport de l' homothétie
Ici donc
Ainsi, quand M décrit le cercle (C), M' décrit un cercle (C') de centre ) et de rayon
. C' est ce qu' on appelle le lieu géométrique de M'
Je te prépare un dessin

Ah merci beaucoup, je ne me souvenais plus de l'homothétie!
Moi je cherchais à résoudre l'exercice juste avec les barycentres, donc je vais aller chercher le bon chapitre pour m'en sortir 
Encore merci de passer du temps libre pour aider les autres!
Ro merci encore! J'ai compris maintenant!
Une petite question : quel est ton logiciel?
Il a l'air plus complet que le mien!
Je vais tout de suite le télécharger et l'essayer!
Si j'ai un problème pour la construction je reviendrai.
Et merci beaucoup pour ton aide 
J'ai une petite question, quand je relis 2 points, il apelle le segement "a" par exemple, et je ne trouve pas comment faire pour qu'on ne voit pas ce"a"
Dans la barre des icones, cherche une icone "Aa"
Tu la cliques et tu cliques sur les objets dont tu ne veux pas voir l' étiquette .

Merci beaucoup, grâce à ton aide j'ai pu finir cet exercice 
Et le logiciel est très pratique!