AB = a
AC = b
BC = x
BD = a

Beta = angle ABC

Pythagore :  a² + b² = x²
sin(beta) = b/x
sin(beta/2) = AD/2a

Donc :  AD = 2a.sin(beta/2)

Reste à faire un peu de trigonométrie et à résoudre une petite équation...

Bonsoir,

D'abord, est-ce [BC] ou (BC)? Il faut préciser. Heureusement, ici, il existe 2 points en même temps D distincts, l'un dans [BC] et l'autre dans (BC) mais à l'extérieur de [BC].
Je vais considérer ici la consigne avec [BC].
Soit B et C deux points distincts du plan et O leurs médiatrice.

L'ensemble des points A tel que ABC est rectangle en A est le cercle de centre O et AB et AC). Tu le trace et tu mets n'importe quel point.

L'ensemble des points D tel que AB=BD est le cercle de centre B et de rayon AB. Tu le trace. Puisque alors c'est l'intersection.

Maintenant, tu choisis un repère (je te conseil le repère (le même O), avec (ou bien c'est la même chose).

Dans ce cas, pour les coordonnés, t'as déjà O(0,0) et B(x/2,0) et C(-x/2,0).BC=x. Il ne te reste pas grand chose. Tu travailles ceci analytiquement (il existe aussi une méthode non-analytique. Que dis-je? Un simple problème peut avoir beaucoup de méthodes!).

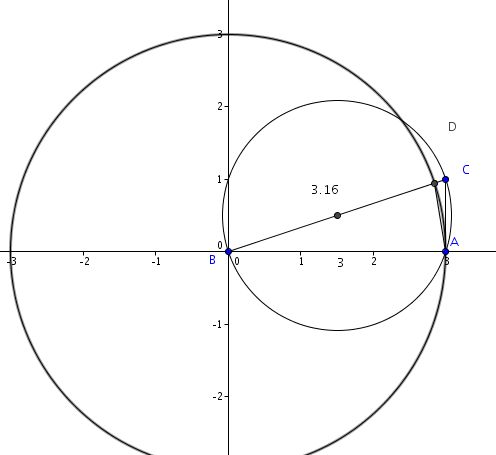
Voici un schéma (ici, x=4, mais tu droit travailler ça pour TOUT b0 (sinon B=C), et A c'est n'importe quel point du cercle) .

Bonne chance!

Désolé, ici:

"D'abord, est-ce [BC] ou (BC)? Il faut préciser. Heureusement, ici, il existe 2 points en même temps D distincts, l'un dans [BC] et l'autre dans (BC) mais à l'extérieur de [BC].
Je vais considérer ici la consigne avec [BC]. "

Justement, c'est exactement la question que je demandais précédemment, je commençais même à me demander si elle avais vraiment de l'intérêt.

L'aire d'un cercle n'est pas celui du point qui est sur sa circonférence.

Je fait ce que tu me dit , j'ai choisis deux cercles avec des valeurs exactes, ils ne sont pas tous comme cela.


et

C'est correcte ce que tu as fait, mais la façon optimisé de le faire, c'est d'avoir de moins de variables possible. C'est le cas que je t'ai donné ici:

Et là j'ai pas payé attention. T'as affaire à des équations cartésienne donc il vaut mieux mettre BC=2a que BC=x (2a pour que je n'ai pas de a/2).

L'équation du cercle de centre O et de rayon OB=OC=a est donc
Tu vois comment ça devient facile?
Continue!

Astuce: A est aussi l'intersection des deux cercle, or ces deux cercles ont 2 points en commum, l'un dans le demi-cercle(de centre O) en haut et l'autre en-bas. Il facile de démontrer que si A est en haut, son équivalent A' est en bas, alors AD=A'D. Donc il suffit d'étudier ce problème dans le demicercle d'en haut, qui signifie que les ordonnés de A sont toujours positifs...

Pour info, en prenant les notations et les pistes que j'ai indiquées à 18h30, le problème se résout en 5 minutes.

AB = a
AC = b
BC = x
BD = a

sin(beta) = AC/BC = b/x
sin(beta/2) = (AD/2)/BD = AD/2a = s

AD = 2a.s

cos(2.beta/2) = cos²beta/2 - sin²beta/2 = 1 - 2 sin²beta/2 = 1 - 2s²

D'où :  AD = a.racine(2 - 2.a/x)

Oui effectivement (j'ai pas payé attention à ce msg dsl^^)
La méthode de LeDino est meilleur!

oui, c'est bien! surtout  AD = a.racine(2 - 2.a/x)

comment tu es passé d'une équation trigonométrique à une équation avec la racine?

On cherche AD tel que :  
sin(beta/2) = (AD/2)/BD = AD/2a

Or :
cos(beta) = AB/BC = a/x
cos(beta) = cos(2.beta/2) = 1 - 2.sin²beta/2
a/x = 1 - 2.sin²beta/2
1 - a/x = 2.sin²beta/2
2 - 2a/x = AD²/a²
AD = a.racine(2 - 2a/x)

bonjour,
dans le triangleABD on peut aussi écrire

c'est la même réponse que le dino.






Dans tout les cas:


Donc ici:



en latex:
\frac{a}{x}=\frac{AB}{BC}=cos(\widehat{B})
\frac{AD}{2a}=\frac{AD/2}{BD}=sin(\widehat{B}/2)
cos(\widehat{B}) = 1 - 2*\sin^2(\widehat{B}/2 )
1-\frac{2*AD^2}{4a^2}=1-sin^2(\widehat{B}/2)= cos(\widehat{B})=\frac{a}{x}

oui c'est la même réponse mais c'est une autre démonstration ,c'est tout

Encore heureux que ce soit la même réponse ...

bonsoir LeDino

Bonsoir veleda .

Je crois qu'on a évité une noyade dans un verre d'eau ...

\sqrt{a²+b²} a>b

a\sqrt{1+b²/a²} on pose b/a=tan x

log tanx=log (b)-log(a)

\sqrt{a²+b²}=a\sqrt{1+tan^2 x}=a sin x