Inscription / Connexion Nouveau Sujet
Triangles isométriques
Bonjour,
je suis en train de réviser le chapitre sur les triangles isométriques. Un des théorèmes indique :
Si deux triangles ont un angle égal (de même mesure) compris entre deux côté respectivement égaux (de mêmes longueurs), alors ils sont isométriques.
Tandis, pour moi, l'angle ne doit pas être forcément compris entre deux côtés. Si on connaîs la position de l'angle, on est capable de trouver la longueur du troisième côté manquant par le théorème de Pythagore généralisé : ). Ainsi, on trouvera toujours le même triangle, où est ce que je me trompe? Existe-t-il un contre-exemple?
??
l'un quelconque des trois angles d'un triangle est forcément
compris entre deux côtés ; et deux côtés sont forcément consécutifs.
Dans a² = b² + c² - 2bc cos( )
)
 est l'angle compris entre b et c
est l'angle compris entre b et c
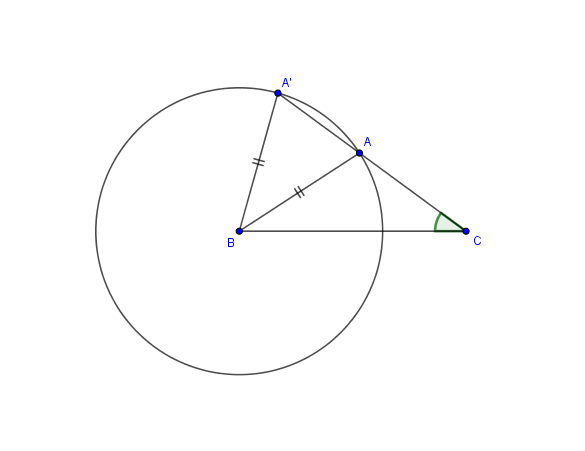
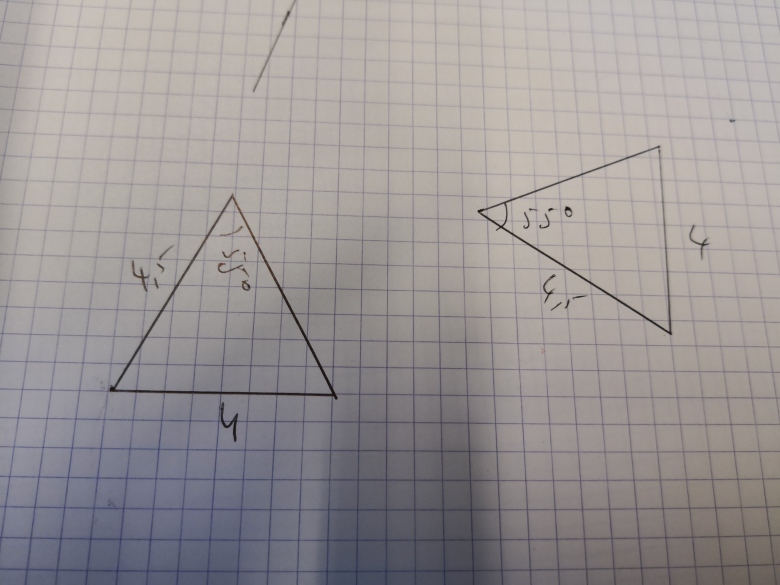
Oui, je suis d'accord qu'un angle est toujours compris entre deux côtés, mais le théorème dit que l'angle égal doit être compris entre les deux côtés égaux. Dans l'exemple ci-dessous:
ils ont deux côtés égaux, mais l'angle égal n'est pas compris entre les deux côtés égaux. Mais pour moi, les triangles sont isométriques, car on a pour le côté inconnu de longueur :
Merci beaucoup, en effet, j'ai oublié qu'on peut trouver deux solutions pour ... (la deuxième n'étant pas toujours à exclure..)
j'ai oublié qu'on peut trouver deux solutions pour
Oui, avec les notations de ma figure, tu peux prouver qu'elle "n'est pas à exclure" lorsque

Dans mon cas de figure, j'avais aussi déjà deux solutions.. Mais à ma première recherche, je n'ai juste pas fait attention aux deux solutions des côtés (j'ai cherché une : 4,13 et je me suis arrêter, car ça correspondait bien à "mon dessin", pourtant, la deuxième possiblité : 1,03 n'était pas non plus à exclure ^^