Bonjour, j'ai un devoir de maths à faire et je bloque sur quelques questions.
Voilà le sujet:

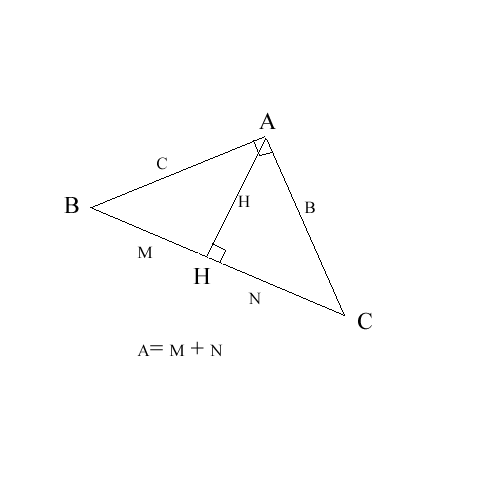
Sur la figure ci-dessous, ABC est un triangle rectangle en A et le point H est le pied de la hauteur issue de A.

1. a) Trouver les 3 triangles semblables (ça c'est bon j'ai su faire quand même)
   b) Les notation etant celles de la figure, établir la relation: h² = m x n. (alors la j'ai cherchais je vois vraiment pas comment trouver ça)
   c) En déduire alors la construction d'un segment de longueur 7 cm. Puis d'une manière générale, celle d'un segment de longueur P, où P est un nombre premier. (je vois pas non plus comment faire. Comment peut on chercher racine de 7 alors qu'il y a aucun chiffre sur le schéma ).

2. a) Montrer que : b²=a x n et c²= a x m (je pense qu'une fois que j'aurai compris comment faire pour h², ces 2 là suivront).
   b) En deduire une démo du théorème de pythagore (je pense que ca doit pas être compliqué mais vu qu'il faut en déduire, et que j'ai pas la 2.a).

Si vous pouviez m'aider ca serai très gentil de votre part, je galère déjà depuis un bout de temps dessus. Merci d'avance !



Edit Coll : symboles