Inscription / Connexion Nouveau Sujet
Triangles semblables
Bonjour,
j'ai des difficultés pour résoudre un exercice :
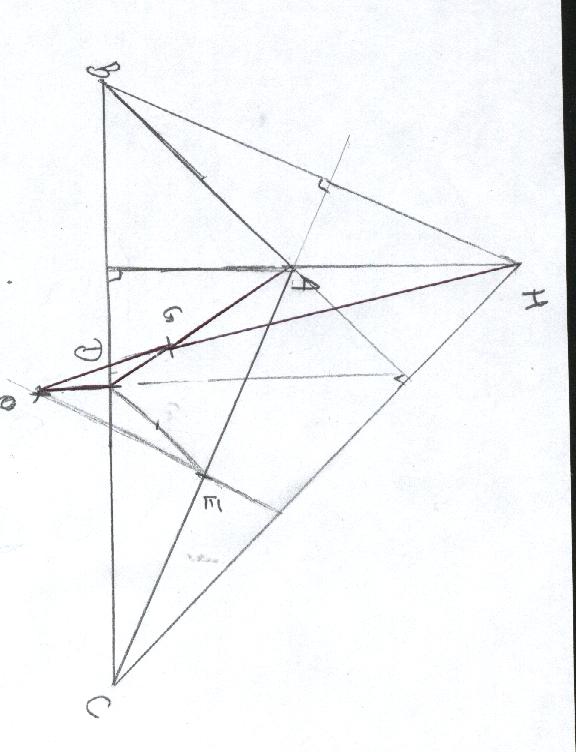
Soit ABC un triangle quelconque,H son orthocentre, O le centre du cercle circonscrit. Soit D et E les milieux respectifs des segments [BC] et [AC] et G le centre de gravité.
1.a).Démontrer que les triangle ABH et DOE sont semblables.
b).Démontrer que AH=2OD.
2.Démontrer ue AGH et DOG sont des triangle semblables.
3.a). Démontrer que les ppoints H,G et O sont alignés.
b). Calculer GH/GO.
J'ai commencé ceci:
1.a).(AB)//5ED). (4ème Cas)
(AH)//(DO). (4ème Cas)
Donc ABH et DOE sont semblables .
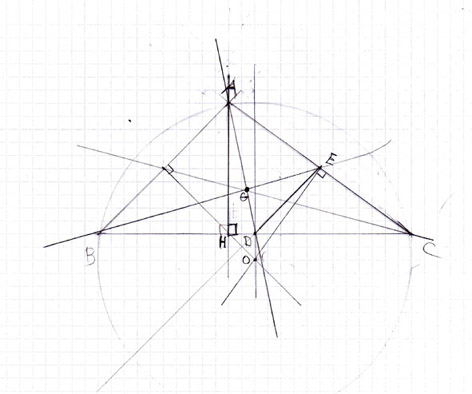
J'ai refait la figure car l'orthocentre est était faux.
Cette fois AH=OD est vrai mais je ne sais pas comment le démontrer.
Merci de m'aider
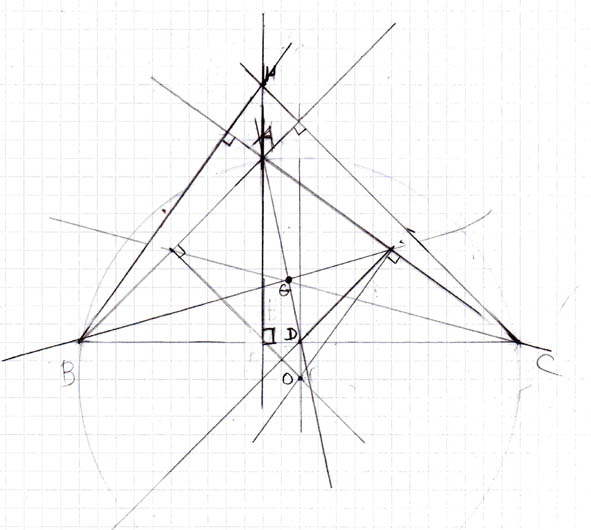
bonjour
1/E est milieu de AC et D est milieu de BC donc d'après le théorème des milieux DE//AB OD est sur la médiatrice de BC donc OD est perpendiculaire à BC, AH est perpendiculaire à BC par construction donc AH//OD,
OE est sur la médiatrice de AC donc perpendiculaire à AC, BH est perpendiculaire à AC donc BH//OE
je te laisse conclure
2/Les triangles ABH et ODE sont semblables il existe un réel k tel que
BH/OE=AB/DE=AH/OD
et AB//DE AC et BC sécantes en C
on peut appliquer Thalès
AE/AC=CD/BC=DE/AB
par construction AE/AC=1/2 donc k=1/2
donc DE/AB=1/2
d'où AH/OD=2 AH=2OD
3/ AG=2GD théorème de la médiane
AH=2OD d'après 2/
il nous reste à définir l'angle en A, AH//OD l'angle en A esqt égale à l'angle en D
les triangles sont semblables
4/b/les triangles AHG et OGD sont semblables
AH=2OD
AG=2GD
d'où HG=2GO
et a/ HG//GO deux droite parallèles ayant un point commun sont confondues donc HGO sont alignés
Merci pour l'aide. Je vais tout récapituler et si j'ai un souci je vous appellerais à l'aide
Merci encore
Désolé, car si je comprends bien jusqu'à Thalès pour le 2), je ne comprends pas comment AH/OD=2 par cette démonstration. Je pensai le faire uniquement en faisant AH = 2OD si je passe OD de l'autre coté de l'égalité je trouvais AH/OD=2. C'était rapide mais je ne comprends pas le rapport avec Thalès. C'est trop bête!!!
Merci
[/b]Tu as AB//DE et AC et BC secantes en C on peut appliqué thalès
AE/AC=CD/BC=DE/AB (1)
or AE/AC=1/2 par construction E milieu de AC
donc les ratios de Thalès valent 1/2 d'une part
ensuite tu as démontré que les triangles ABH et ODE sont semblables
Il existe un réel k tel que
BH=kOE
AB=kDE
AH=kOD
donc BH/OE=AB/DE=AH/OD (2) d'autre part
en mettant en commun les deux
tu as d'après (1) AE/AC=1/2 donc [b]DE/AB=1/2
et d'après (2) AB/DE=AH/OD donc OD/AH=1/2
donc OD=1/2AH AH=2OD
J'ai compris mais j'ai du mal à visualiser les triangles HDA et EDO. C'est pourquoi je perds le fil. Pour l'instant je comprends. Je continue mon exercice. A plus tard. Merci
Pour le 3) je ne trouve pas pourquoi l'angle A = l'angle D. Par contre par thalès l'angle G est commun aux deux donc ils sont semblables. Est-ce que cette définition est bonne? Merci
Pour le 3/b j'ai bien compris. Merci. J'attends votre correction pour 3) triangles semblables avec angle G commun. A bientôt.
tu as deux parallèle et un droite sécante
http://img156.imageshack.us/img156/6526/triangle001rc5.jpg
(utilise ce lien pour ouvrir l'image; surligne, clique droit, "copier" => dans ta barre de navigation qui affiche "https://www.ilemaths.net/sujet-triangles-semblables-193050.html" clique droit puis sur "sélectionner tout" et enfin "coler"; appuie sur entrer et tu verras la figure.)