Bonjour quand même...

Que proposes-tu pour la réponse à la première question ?

Il faut utiliser le théorème de l'angle inscrit !
Pou le 2nd exo l'angle A est partagé par la bissectrice et les angles B et C sont égaux, l'angle au centre y est pour qqch ! Rep Moi pour l'exo 1 stp !

Je ne comprends pas ta démonstration.

Pour démontrer que les triangles ACI et BAE sont semblables tu peux démontrer qu'ils ont leurs angles de même mesure.
Comment le démontres-tu ?

Pour l'angle BAE et CIA ils sont égux car ils sont coupés par la bissectrice.
Apres je vois pas trop comment prouver pour les autres angles !
Tu aurais une idée toi ?

Pourquoi ces deux angles et ont-ils même mesure ?

Pourquoi ces deux angles et ont-ils même mesure ?

Eventuellement (ce n'est pas obligatoire) :
Pourquoi ces deux angles et ont-ils même mesure ?

A faire de préférence dans cet ordre...

BAE et IAC sont égaux cai ils sont coupés par la bissectrice sachant qu'une bissectrice partage 2angles de meme mesure.
Pour les angles ABE et AIC je pense que c'est le théoreme de l'angle inscrit.
Ils interceptent l arc de cercle BI donc ils sont égaux.
Qu'en penses tu ?

Oui pour les deux premiers : c'est bien une propriété d'une bissectrice.

Pour les deux suivants : et ils interceptent le même arc AC ; le théorème des angles inscrits permet de conclure qu'ils sont égaux

Cela suffit à démontrer que les triangles ABE et AIC sont semblables.

Les deux derniers angles : et ont même mesure car dans un triangle la somme des angles vaut 180°
Si les deux premiers angles ont même mesure deux à deux alors obligatoirement les derniers angles ont aussi même mesure. Mais c'est pour cela qu'il n'est pas nécessaire de l'indiquer dans la démonstration.

Deuxième question : je pense que tu sais la faire tout(e) seul(e) maintenant ; elle ressemble beaucoup à la première...

J'appréçierai de l'aide pour la 2eme question !
Faut-il utiliser le théorème de l'angle inscrit ?
Si oui, qu'est ce que j'ai avec les 3données : AB=9.6 AC=5 AI=8 ?
Merci
Sans indiscrétion es tu un prof de math parce que tu es fort ?

Les données des trois longueurs ne seront utiles que pour la troisième question.

Deuxième question : pour montrer que ces deux triangles sont semblables il faut, comme pour la première question, montrer que des angles sont égaux.

Montre que ... évident ! Parce que ...

et montre que en n'oubliant pas ce que tu as vu à la première question

ou bien :
et montre que toujours en utilisant le résultat de la première question

AIC = CIE car c'est le meme angle .
IAC = CIE car ils interceptent le meme arc de cercle AC ! C'est ça ?
Quand a ACI = CEI je ne vois pas !

D'accord pour le premier couple : c'est le même angle

Tu ne fais pas attention aux noms des angles ; ce ne sont pas IAC et CIE ; ces deux angles ne sont pas égaux, c'est



N'oublie pas les hypothèses ! AI est bissectrice !



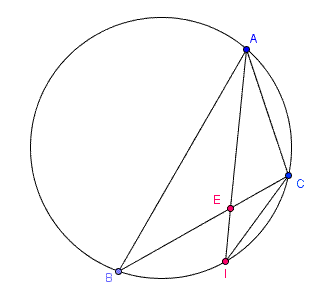
La figure est à l'échelle ; mais elle est là pour illustrer la troisième question.

Pourquoi IAC = ICE ? Car ils interceptent l'arc de cercle AC ?

Une autre question: pour prouver que AEC = CEI comment je peut le démontrer ?
Est ce que j'ai le droit de dire que étant donné qu'ils sont sur [AI] la somme des 2 et égale à 180° ?

Ce n'est pas le tiercé !

Quand on met les trois lettres qui désignent un angle dans le désordre plus personne ne comprend rien. Je ne comprends plus rien à ce que tu écris.

Comment prouver que IAC est égal a ICE ? Et AEC est égal à CEI sachant qu'ils sont sur le segment[AI]
ils doivent etre egal a 180°

n'est pas du tout égal à

En effet la somme des mesures de ces deux angles vaut 180°
Mais on n'a pas besoin de ce résultat.

Mais alors si ils ne sont pas égaux comment prouver que les triangles sont semblables ?????????

Pour prouver que les triangles ACI et CEI sont semblables il suffit que tu démontres que deux des trois égalités de mesures d'angles ci-après sont vraies. A toi de choisir et de ne pas te tromper dans l'ordre des lettres !

Il faut démontrer que ACI = CEI
que IAC = ICE
mais par quel moyen ? theoreme de l'angle inscrit ?

Tu n'as pas choisi les plus simples, mais c'est ton choix.

Pour démontrer que

il faut utiliser le résultat de la première question. Comment fais-tu ?

Pour démontrer que

il faut en effet à nouveau les angles inscrits, sans oublier que AI est une bissectrice

Je n'arrive pas pour les angles ACI et CEI !!
Pour la bissectrice elle l'est que pour l'angle BAC par pour EIC !
Aide moi !! Je suis pedu la !!

Est ce que ça serait possible d'avoir ton mail en cas de probleme en maths Pour les prochaines fois si prochaines fois il y a ??

Pour démontrer que :
Tu as démontré à la première question que les triangles ACI et AEB sont semblables ; donc
et comme parce que ce sont des angles opposés par le sommet
alors
____________________

Pour démontrer que :
c'est le même angle !
____________________
Pour démontrer que :
Puisque la droite AI est bissectrice de l'angle les angles et ont même mesure et en conséquence les arcs qu'ils interceptent, les arcs BI et IC sont égaux
L'angle intercepte l'arc IC
L'angle intercepte l'arc IB
Donc les angles et ont même mesure.
____________________

Donc les triangles ACI et CEI sont semblables.

Pour la question petit 3 quel théoreme faut il utiliser ?
Peu tu me confirmer que c'est Pythagore ??!!!!

Aussi je n'ai pas bien comprit ! Pourquoi l'angle IAC intercepte larc IC ?? Sur le shéma l'angle IAC est opposé à cet arc ! non ?
Merci beaucoup quand meme !

Il n'y a aucun triangle rectangle. Donc... pas de Pythagore

La troisième question se fait en utilisant les triangles semblables qui ont été démontré aux deux premières questions. Tu peux écrire de nombreuses égalités de rapports de longueur des côtés. Et ainsi de proche en proche tu trouves toutes les longueurs.

Désolé de autant t'embeter mais je n'ai jamais vu d'égalités de rapport de longueurs des cotés !!
Malgré avoir revue mon cours de 3eme je ne vois pas du tout !!!

j'ai un autre exo ou j'ai un probleme!
2cercles C et C' se coupent en I et J.
On désigne A,B 2pts de C distincts des points I,j
(JA) recoupe C' en A'
(JB) recoupe C' en B'
démontrer que IAB et IA'B' sont semblables
moi j'ai dit que d'apres le theoreme de l'angle inscrit A'IB'= AIB car ils interceptent l'arc de cercle A'J
apres pour les derniers angles je n'arrive pas.