Inscription / Connexion Nouveau Sujet
triangles semblables
Bonjour à tous 
J'ai un exercice qui doit se traiter avec des triangles semblables mais je ne vois pas du tout comment !
Le voici :
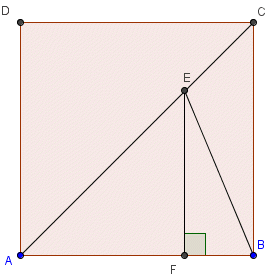
On a un carré ABCD de coté a.
E un point du segment AC tel que AE=a.
Et il faut montrer que aire(AEB)/aire(ABCD) est un irrationnel .
Surement qu'il faut utiliser que la diagonale d'un carré de côté a est irrationnelle, mais j'aimerais comprendre comment utiliser les triangles semblables dans cet exo !!
Merci d'avance 
bonjour,
AEB est un triangle isocèle en A avec AB=AE=a
soit H le pied de la hauteur issue de A relative à (BE)
ABCD est un carré-->BAC=BAE=45/2=22.5°
cos22.5=AH/AE-->AH=...........
sin225.5=HE/AE--->HE=..........
A(ABE)=AH*2HE/2
Il y a une solution beaucoup plus simple que ça, pas besoin d'utiliser de trigo, on peut tout faire avec les valeurs exactes ...
Certes, le terme de "projection orthogonale" se voit peut-être plus tard, alors je change d'expression :
Dans le triangle ABE, appelons F le pied de la hauteur issue de E.
Et voilà, un élève de 5ème comprend ! 
Merci 
Mais donc ça n'utilise pas les triangles semblables ...
Enfaite je cherche un exercice pas trop trivial sur les triangles semblables et les aires.
Et celui ci était dans le chapitre triangle semblable, c'est pour ça..