Inscription / Connexion Nouveau Sujet
Trigo et algo
Bonjour,
Mon professeur de mathématiques nous as envoyé un DM que j'ai beaucoup de mal a comprendre. La dernière question parle d'algorithmes mais nous ne l'avons jamais vu en classe... J'ai essayer de me débrouiller comme je pouvais pour la première question mais sa m'étonnerait d'avoir trouvé quelque chose de juste...
Voici mon DM:
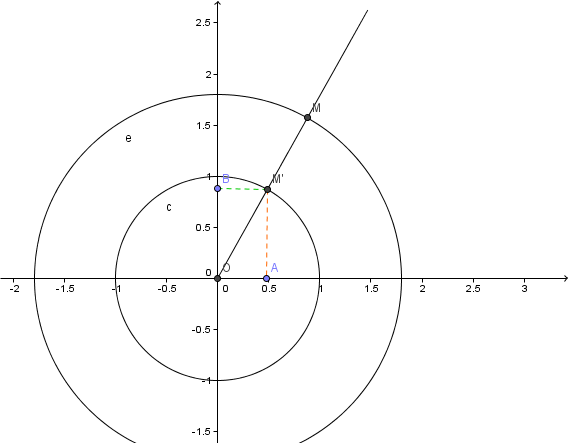
Etant donné un repère orthonormé (O, I, J), M le point appartenant au cercle de centre O et de rayon R, avec R > O.
L'angle IOM vaut α degrés avec 0°≤ α ≤360°.
La demi droite [OM) rencontre le cercle de centre 0 et de rayon 1 en M'.
1)En notant x la mesure,en radians,de l'angle IOM' déterminer les coordonnées de M' en fonction de x puis celles de M en fonction de x et de R.
2) Ecrire un algorithme qui, après avoir demandé un rayon R et un angle α en degrés, retourne les coordonnées de M .
Donc, si [OM) rencontre le cercle trigonométrique en M', ( car un cercle de rayon 1 est trigonométrique) alors [OM']=1 et OMM' sont alignés donc OM=kOM'
Je sais aussi que m(IO,OM')=x.
Mais comme OMM' sont alignés alors m(IO, OM)=α
Donc 0 rad ≤ α≤2π
Mais je ne sais pas quoi faire de ça et je ne sais pas si sa peux même m'aider...
Merci 
bonsoir,
dans le triangle OM'A, rectangle en O,
cos x = OA/OM' = OA/1 = OA
or OA , c'est l'abcisse de M'
donc M' a pour abcisse cos x
tu es d'accord avec ça ?
exprime de meme sin x pour exprimer l'ordonnée de M'
tu auras alors répondu à
En notant x la mesure,en radians,de l'angle IOM' déterminer les coordonnées de M' en fonction de x
puis pour les coordonnées de M, si tu ne trouves pas tout de suite, trace les pointillés des coordonnées de M (comme je l'ai fait pour M') et applique Thalès.
J'ai juste une question, quand vous dites rectangle en O, je ne comprend pas... Je pensais qu'il serai rectangle en A.
Sin(x)=AM'/OM=AM'/1=AM'
Or AM' est l'ordonnée de M'
Donc M' a pour ordonnée sin(x)
Les coordonnées de M'(cos(x);sin(x)).
C'est bien ça ?
je vais bientôt devoir quitter..
as tu trouvé M(R*cos(x) ; R*sin(x)) ?
l'algorithme ?
d'abord on voit comment on fait sans algo :
si tu as R et x, pour trouver xM tu effectues : R*cos(x) et pour trouver yM : R*sin(x)
en algo (langage naturel), ca donne :
R est un nombre
x est un nombre (===> compris entre 0 et 360)
xM, yM sont des nombres
lire R
lire x
xM prend la valeur R*cos(x)
yM prend la valeur R*sin(x)
afficher xM
afficher yM
fin
tu vois ?
J'avais trouvé M(cos(x)/R;sin(x)/R)
Mais je vais recalculer pour trouver votre résultat...
Pour l'algorithme je n'ai pas très bien compris mais je vais reprendre pas à pas pour l'assimiler.
Merci beaucoup pour votre aide, elle m'a été précieuse ! 
regarde la figure :
si M' a pour abcisse cos(x)= OA, et que R=3 par exemple,
ta réponse donnerait xM = OA/3 ==> soit un tiers de OA.. ça ne colle pas. Si R est plus grand que 1, xM est plus grand que xM'.. tu es d'accord ?
si on trace les pointillés pour placer C, abcisse de M
dans le triangle OCM rectangle en C (  ), on a
), on a
cos x = OC/R ==> OC = R*cos x
OK ?
pour l'algo, on fait faire à la machine exactement ce que tu fais toi même comme calcul. ni plus, ni moins.
Sauf qu'on le lui dit en détail (parce qu'elle ne fait que ce qu'on lui demande, elle n'a aucune initiative !).
bonne journée,
je reviens cet après midi pour voir si tu as terminé.
Le fait ai que je n'ai (toujours) pas une calculatrice lycée, ça me pose une problème ou je n'en ai pas besoin?
Donc pour récapituler la première question,
M'(cos(x);sin(x))
M(R*cos(x);R*sin(x))
J'ai toutes les démonstrations donc elle est finie.
Pour l'algorithme, je n'ai que a écrire en détaillant chaque points des démonstrations ?
l' algo (langage naturel), ca donne :
R est un nombre
x est un nombre (===> compris entre 0 et 360)
xM, yM sont des nombres
lire R
lire x
xM prend la valeur R*cos(x)
yM prend la valeur R*sin(x)
afficher xM
afficher yM
fin
à toi de rédiger !
bonne journée