Inscription / Connexion Nouveau Sujet
Trigo et complexes
Bonjour !
Je viens pour cet exercice :
Soit A, B, C, D les points d'affixes respectives : a=8, b=8i, c de module a et d'argument - /3 et d=b
/3 et d=b [cos (2
[cos (2 /3) + isin(2
/3) + isin(2 /3)].
/3)].
PARTIE A : 1) Déterminer les formes algébriques de c et d.
2) Montrer que A, B, C, D sont sur un même cercle dont on précisera le centre et le rayon.
On note z1 l'affixe du vecteur AC, z2 l'affixe du vecteur BD, z3 l'affixe du vecteur AB et z4 l'affixe du vecteur DC.
a) Montrer que z2=z1 3.
3.
b) Calculer |z3| et |z4|
c) Montrer que le quadrilatère ABCD est un trapèze isocèle.
PARTIE B : e est le nombre complexe de module  2 et d'argument
2 et d'argument  /4.
/4.
1) Déterminer la forme algébrique de e.
2) Calculer la forme algébrique de c e.
e.
3) Quelle est la forme trigo de ce produit ?
4) En déduire les valeurs exactes de cos(- /12) et sin(-
/12) et sin(- /12).
/12).
Je ne comprends déjà pas très bien l'énoncé pour répondre à la 1ère question, je pense qu'il faut d'abord avoir la forme trigo de a mais son argument est nul puisque son ordonnée est aussi nul. Même pour l'argument de d qui est égal à b, je ne comprends pas très bien.
Merci d'avance !
Bonjour,
A.1) On te demande la forme algébrique de , de module
et d'argument
: cela me semble une application directe du cours.
On te demande également la forme algébrique de
Je ne vois pas bien la difficulté non plus.
1) Ce qu'on demande, ce sont les formes algébriques de c et d .
Note que b ne peut être ni l'argument, ni le module de d , car b , qui est égal à 8i , n'est pas un nombre réel.
En fait, l'expression de d est encore différente :
d = 8i(cos2 /3 + isin2
/3 + isin2 /3)
/3)
= 8(- sin2 /3 + icos2
/3 + icos2 /3)
/3)
= 8(-  3 /2 - i/2)
3 /2 - i/2)
= - 4 3 - 4i .
3 - 4i .
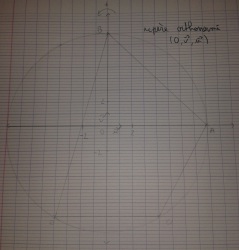
D'accord, j'ai donc placé les 4 points et j'obtiens un cercle de rayon 8 mais est-ce que je dois le prouver par des calculs ?
Un cercle de rayon 8 : cela vient du fait que les affixes des quatre points ont tous leur module égal à 8.
D'accord, aussi j'ai un problème car normalement je devrais trouver un quadrilatère isocèle, or ce n'est pas le cas ici :