salut

il faut chercher T , tel que f(x+T)=f(x)

sachant que cosinus et sinus sont 2pi périodique

et tangente est pi périodique..

à toi de jouer.

Merci pour la réponse mais disons que je savez que pour trouver le période T il fallait un réel T appartenant à R tel que f(x+T)=(x)

mais dans une fonction bien déterminée je n'arrive pas a trouver le T pour chaque membre de la fonction on parle de période commune.


merci pour le reponse ...

c'est au minimum 2pi d'après les indices que je t'ai donné !

je suis désolé de te déranger disdrometre mais je comprend pas par exemple j'ai ma fonction f(x)= cos(2x)-sin²(x)+tan²(4x) comme trouver la période de celle-ci. Pourrai tu si cela ne te derange pas me faire par d'une méthode? je vous remercie.

Bonjour,
Essaie d'appliquer la formule: cos(a+b)=cosa*cosb-sina*sinb
Remplace b par T pour touver cos(a+T)= cos(a). Bon courage.

dans ce cas je regarde chaque période des 3 fonctions et je prends la période la plus longue ou une combinaison des périodes

cos(2x + 2pi)= cos(2x)  =>  cos(2x) est pi périodique
sin^2(x+pi) = sin^2(x) =>  sin^2(x)  est pi périodique
tan^2(4x) = tan^2(4x+pi) =>  tan^2(x) est au moins pi/4 périodique

donc f est pi périodique ..

je viens à l'instant de le faire certes pour une fonction tel que cos(x) ou si(x) sa marche mais pour une somme ouun produit de fonction trigonométrique comment faire pour déterminer la période de la fonction en question?


Je vous remercie...

pour le cos tu voulais pas plutot dire

cos(2x + 2pi)= cos(2x)  =>  cos(2x) est DEUX pi périodique  ???


et dernier truc dis mois juste comment tu sais que tan²(4x) et pi/4 périodique ??? détail svp !!!  merci infiniment.

non t'avais raison désolé j'avais oublié le 2 devant le x.

puisque
tan(x+pi) = tan(x)

donc

tan(4x+pi)= tan(4x)

or 4x+pi = 4(x+pi/4)     donc pi/4 périodique..

merci infiniment je pige parfaitement désormais merci encore.

Bonne soirée et bon courage au revoir .

cos(2x) = cos(2x + 2pi) = cos(2(x+Pi)) --> est Pi périodique.

sin(x) = -sin(x+Pi)
sin²(x) = sin²(x + Pi) --> est Pi périodique.

tan(4x) = tan(4x + Pi) = tan[4(x + Pi/4)]
tan²(4x) = tan²[4(x + Pi/4)] --> est Pi/4 périodique

Le PPCM de Pi et Pi/4 est Pi -->

f(x)= cos(2x)-sin²(x)+tan²(4x) est Pi périodique.
-----
Sauf distraction.  

bonjour

n'hésite pas à te faire confirmer avec ta calculatrice graphique :



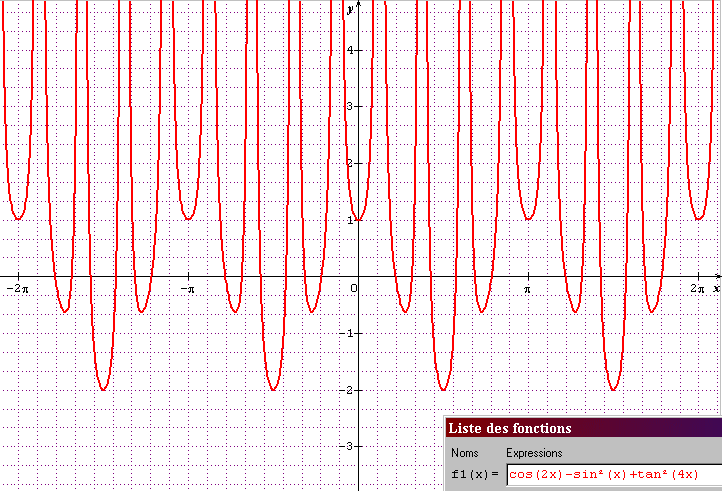
il semble bien que PI soit la période

salut mika

je n'aime pas trop ce genre de preuve, si j'étais un poil pointilleux, et qu'est qui se passe pour y> 6 ?
c'est encore périodique ?

je suis d'accord avec toi DD-bonjour-, sauf que je n'ai pas parlé de preuve...

juste une confirmation, voire une indication d'axe de recherche, pas plus...

par ailleurs, avec des fonctions trigo uniquement ( pas de y = x - sinx ... ), y'a de grandes chances que ce soit périodique, même au delà de l'axe des abscisses

-------------

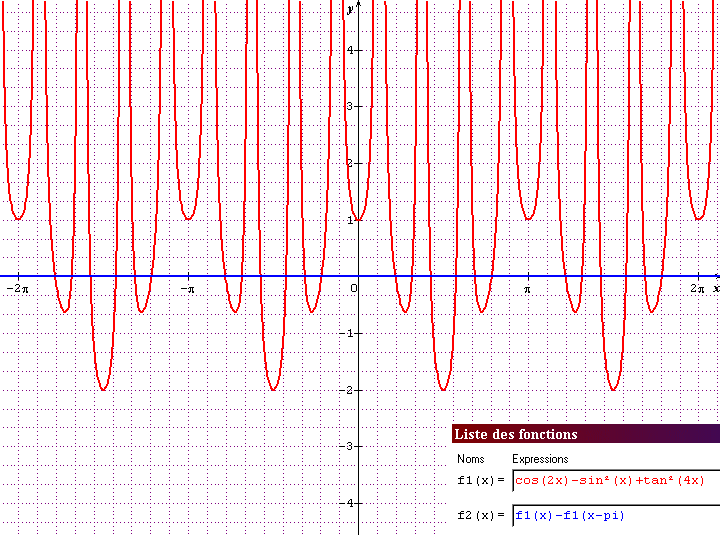
par ailleurs, Sine Qua Non est assez puissant pour, par exemple, permettre la soustraction entre une fonction f(x) et f(x-T)

si T est un multiple de la période, f(x)-f(x-T) doit être nul; ce qui est bien le cas ici ( f2(x) = f1(x) - f1(x-pi) ) :