Inscription / Connexion Nouveau Sujet
Trigonométrie dans un Carré
Bonjour j'ai cet exercice en devoir maison a faire pour demain mais je bloque un peu et j'aurais besoin d'un coup de pouce si vous avez du temps.
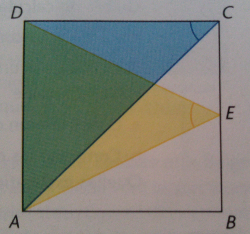
ABCD représente une salle de spectacle carrée de côté a , dont la scène est représentée par le segment [AD].
Cathy et Eloïse sont placées respectivement aux points C et E , le point E étant le milieu du côté [BC].
Elles comparent l'angle sous lequel chacune d'elles voit la scène ( ACD et AED ).
Chacune prétend avoir l'angle de vue plus grand que l'autre. Qui a raison ?
Ce que j'ai déjà fait :
Etant donné que ABCD est un carrée , tout ses angles font donc 90°
Comme AC est une droite qui coupe le carré ABCD en deux parts égales on peut donc en déduire que l'angle ACD = 45° car 90 / 2 = 45°
Après pour ce qui est de l'angle AED je ne sais pas par quel moyen je peut le trouver et donc prouver qui a raison...
Quelqu'un peut il m'aider ?
Bonjour,
calculer l'angle CED par la trigonométrie (tangente)
et BEA est le même et donc AED = 180° - 2 CED
Okay je vois comment vous voulez procéder , mais comment utiliser la tangente sans aucune autre mesure que 45° ( qui est ACD)
Il me faudrais trouver CDE pour pouvoir en déduire E seulement je vois pas vraiment comment calculer / trouver CDE ...
E étant le milieu de BC on a EC = BC/2 = AC/2 soit AC/EC = 2
définition de la tangente dans un triangle rectangle ...
CDE on s'en fiche, ce serait une autre méthode.
Je te parlais de l'angle CED que tu obtiens en calculant sa tangente.
trigo, c'est bien dans le titre non ???)
à propos de CDE dans le même triangle rectangle tu peux calculer CDE lui aussi par sa tangente, même méthode.
et tu as directement l'angle DEA = 2*CDE (voir triangle isocèle DEA, la bisectrice est hauteur, parallèles, angles alternes-interne etc)


