Inscription / Connexion Nouveau Sujet
Trigonométrie dans un triangle inscrit dans un cercle
Bonjour à tous !
J'ai un exercice à faire pour vendredi, et je n'arrive pas à faire la dernière question qui consiste à démontrer deux égalités :
- Montrer que = 75°
- Montrer que : sin 75° = (
+1)
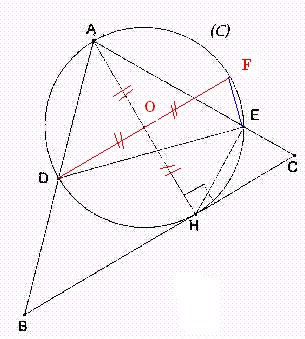
Voici le dessin : ***
Si vous avez besoin d'autres mesures d'angles ou de longueurs, demandez-moi et je les calculeraient !
Je vous remercie d'avance pour votre aide !
bonjour
tu aurais du recopier le texte de ton énoncé en entier...
Philoux
Désolé, j'ai le bras dans le platre 
Il faut que j'attende mon père
pour quelqu'un qui a le bras dans le plâtre, tu maîtrises bien LaTeX ...
Philoux
Merci mais c'est mon père qui l'a tapé !
Il vous faut des mesures pour démontrer les égalités ?
S'il vous plait ...
Merci pour votre aide, si vous avez une raison pour ne pas me répondre je vous écoute !
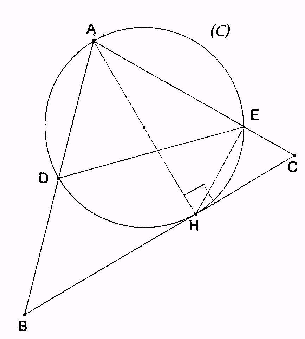
Je complète ton énoncé. Normalement, il faut le recopier...
= 45° et
= 30°
AH = 6 cm
A vue de nez, est un angle droit (intercepte un diamètre) et il y a des angles inscrits qui interceptent le même arc, et qui sont donc égaux.
Mais pour la suite, il faut que quelqu'un d'autre t'aide, la trigo n'est pas mon fort 
M'enfin, un bras dans le plâtre, ça n'empêche pas de pianoter sur un ordi 
Bonjour,
Il y a deux angles à 75° mais le plus pratique est pour trouver sin 75°.
On sait que =45° et que
est un angle droit donc
= 45°
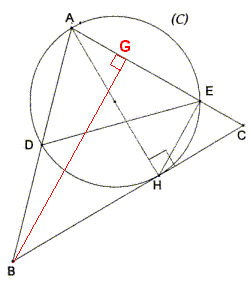
On construit un triangle BAG tel que BG soit la hauteur du triangle BAC depuis le sommet B et en plaçant G sur AC.
Comme est un angle droit alors
= 15° et
= 30° ( on a trouvé plus haut :
= 45° )
Pour trouver BG :
HC = AH.tan30° =
BH = AH = 6
BC = BH + HC = 6+ = 6(1+
)
BG = BC.cos30 = 6(1+).
= 3(
 3+1)
3+1)
BA = AH/cos45°=6.2/ 2=6
2=6 2
2
sin 75° = sin = BG/BA = ....
cqfd
On peut vérifier avec la formune sin(a+b) = sinacosb + cosasinb (a=30° et b=45°)
A+, KiKo21.
Si on utilise = 75° ,
on trouve sin 75° =
C'est bien la valeur recherchée, mais je n'ai pas trouvé comment mettre le résultat sous la forme demandée...
Si quelqu'un a la solution... borneo peut-être ??
A+, KiKo21.
bonjour
V(2+V3) = V[( 4+2V3 )/2] = V[( 1+2V3+3)/2] = V[(1+V3)²/2] = (1+V3)/V2
Sauf erreur...
Philoux
Salut borneo,
Pas besoin pour répondre à ma question !
Juste montrer que :
Comment tu trouves mon latex débutant ?
sinon pour sinus et cosinus, j'utilise toujours le cri du triangle rectangle :
SOHCAHTOA !
SOH : sinus=côté opposé/hypothénuse
CAH : cosinus=côté adjacent/hypothénuse
TOA : tangente=côté opposé/côté adjacent
C'est vrai que ça ressemble à un nom de volcan ou d'île... une île volcanique ?
A+, KiKo21.
Bonjour philoux,
Merci, c'est exactement ce que je cherchais. J'avais commencé dans cette voie mais je ne trouvais pas le terme au carré...
Il y a des jours où on n'a pas les yeux en face des trous (1h de sommeil en moins depuis samedi !!)
A+, KiKo21.
Salut kiko
depuis samedi ou dimanche ? 
Philoux
...depuis la (courte) nuit de samedi à dimanche dernier !!
Mon PC n'a pas été perturbé, lui.
La première chose qu'il a fait dimanche matin, c'est remettre son horloge à l'heure.
J'ai bien essayé moi aussi, mais la mienne est biologique !!
Je vous remercie énormément pour vos réponses !
Encore désolé pour l'énoncé
Longue vie à ilemaths ! ! !
Salut Kiko21, magnifique ton latex. Je m'y mets aussi, j'ai une feuille de traitement de texte avec des modèles que je modifie suivant les besoins. J'ai même fait des tableaux 
Rien que pour toi, borneo :
Si on épelle tous les nombres en Anglais (zero, one, two, three, four, five, six, seven, eight, nine, ...) jusqu'où faut-il aller pour trouver la lettre A ?
Philoux
Marcovolcom (mon fils, mathîlien occasionnel) dit : twelve and a half 
On ne l'a pas envoyé trois mois aux States pour des prunes...
juste une question ke ca pe interresser ou pa simplement ki é bon mm tré si vous voulé en anglais please!i would like help!
thanks very much!
kiss!