Bonjour !

J’ai un exercice de trigonométrie que je n’arrive pas à faire, (cela fait maintenant 5 jours que j'essaie de le résoudre)
Énoncé :
(ici vous trouverez la figure : **** )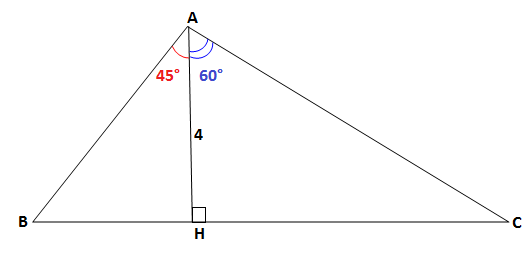

_{* Tom_Pascal > image placée sur le serveur de l', merci d'en faire autant la prochaine fois Dounie *}

1) Calcule les valeurs exactes de BH, BA, CH et CA
2) Déduisez-en que :
périmètre (ABC)=4(v3+v2+3)

J’ai déjà résolu le petit 1) de l’exercice , c’est le petit 2) qui me bloque ,
mais pour le résoudre j’ai donc procédé à la manière suivante :

*J’ai additionné toutes les longueurs (résultats des réponses précédentes)ce qui me donne  

(ABC)= (AB)+(AC)+(BC) = (2v8+2v7+8v3)

1)  j’ai d’abord réduis tous les nombre au même carré (comme pour les fractions), et j’ai utilisé le P.P.M.C (plus petit multiple commun) qui est « 168 »  

j’ai trouvé :
(ABC)= 2v8(x21) + 2v7(x24) + 8v3(x56)
      = 42v168 + 48v168 + 448v168
      = 538v168

2) En trouvant le résultat j’avais prévu de factoriser le tout, pour trouver
périmètre (ABC)=4(v3+v2+3)


Mais c’est là que je bloque, car je crains que mes réponses soient fausses et j’ignore comment résoudre correctement ceci.
Quelqu’un pourrait-il m’aider s’il vous plait ?

P.S.: "v" signifie "racine carré"
      "x" signifie "fois" (multiplier par)
Merci d'avance