Enoncé ambigü.

Je suppose que A appartient à la droite passant par H et perpendiculaire à l'axe des abscisses ainsi qu'au cercle trigonométrique.



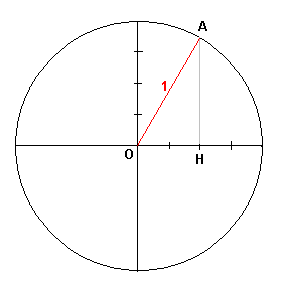
Pythagore dans le triangle AHO avec OA = 1 et OH = 1/2 ...

je te remerci de ton aide!

mais au faite comen tu veut que je fasse pythagore si je cherche le coté ah?

Tu pousses là.

OA² = AH² + OH²

et tu sais que OA = 1 et OH = 1/2

...

désolé donc ensuiite ca fé ca:


OA²=AH²+OH²
1²=AH²+0.5²
AH²=1-0.25
AH²=0.75

c'est bien ca?

Oui mais on te demande AH et pas AH²

a ui exact merci beaucoup

re bonjour,je suis embeter avec cet question(toujours le meme exos donc meme enoncer)


calcule la valeur exacte de AI.quel est la nature du triangle OAI.

(je pense que que AI vaut 1 donc on aurait un triangle equilateral.mais je n'arrive pa a demontrer.aider moi svp merci)

Oui, par Pythagore dans le triangle AHI, on trouve AI = 1

On a donc AI = OA = OI = 1

Et donc le triangle OAI est équilatéral.

ok je te remerci et je comprend pa une autre question encore:
c'est toujours le meme exos

en deduire les valeurs exacte de cos(pi/3),sin(pi/3),tan(pi/3)

merci d'avance.

Dans le triangle rectangle AOH:

AH = OA.sin(AOH)
OH = OA.cos(AOH)
AH = OH.tan(AOH)

Or comme le triangle OAI est équilatéral, ses angles mesurent chacun 60°, soit Pi/3 --> Angle(AOH) = Pi/3, On a donc:

AH = OA.sin(Pi/2)
OH = OA.cos(Pi/3)
AH = OH.tan(Pi/3)

(V3)/2 = 1.sin(Pi/3)  (Avec V pour racine carrée).
(1/2) = 1.cos(Pi/3)
(V3/2) = (1/2).tan(Pi/3)

sin(Pi/3) = (V3)/2
cos(Pi/3) = 1/2
tan(Pi/3) = V3
-----
Sauf distraction.