Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. SecondeForum de Maths Seconde TrigonométrieTopics traitant de trigonométrie [tout]Lister tous les topics de mathématiques
Niveau seconde
Partager :

Trigonometrie et fonction circulaire!

Posté par
christine1635 19-05-07 à 15:56

slt tt le monde!!

g besoin d'aide pour mon exo de math car d'après multiples tentatives je n'ai toujours pas réussi à résoudre les problèmes

j'ai plusieurs questions:
Exo 1: sachant que cos/12 = (6+ 2)/4, calculer la valeur exacte de sin /12

Exo 2: Simplifier les expressions suivantes: cos(--x); sin (x-/2; cos au carré(-x) + sin au carré(-x)

Exo 3: Soit x un réel tel que cos x différent de 0. On appelle tangeante de x le réel noté tan x et défini par: tan x= sin x/cos x. De ce fait, tan x est définie lorsque x est différent de /2 + k (où k est un entier relatif).

1/ calculer tan x pour x=/6 ; /4 ; /3.
2/ Soit x un réel de l'intervalle [/2 ; ] tel que sin x = 3/5. Calculer cos x et tan x.

Si vous arrivez à m'aider sur ca franchement merci bokou, si il y a une matiere ou je pe vous aider, n'hésitez pas jsré la !! merci a tout ce qui vont m'aider!!

Posté par
bruschetta1re : Trigonometrie et fonction circulaire! 19-05-07 à 16:17

cos/12 = (6+2)/4
cos²/12 = (6+2)²/4²
= (36+(2*6*2)+4)/16
= (40+212)/16

cos²/12 + sin²/12 = 1
sin²/12 = 1 - cos²/12
sin²/12 = 1 - ( (40+212)/16 )
= [16 - (40+212)] / 16
= (-24 - 212) / 16

sin/12 = (-24 - 212) / 4

à verifier

Posté par
christine1635re bruschetta! 19-05-07 à 16:19

merci bokou!! moi aussi j'ai trouvé kelke choz dans ce genre la mais je n'étais pas très sur!! tu es en quelle classe?? é pour le reste tu as une idée ou pa??

Posté par
patrice rabillerre : Trigonometrie et fonction circulaire! 19-05-07 à 16:19

Bonjour,

Pour l'exo 1, il faut utiliser la relation cos²x+sin²x=1. On peut en déduire la valeur exacte de sin²(/12) :

sin²(/12)=1-cos²(/12).

Ensuite, il est facile d'en déduire sin(/12) ...

Pour l'exa 2, il suffit de faire un dessin du cercle trigonométrique.

Pour l'exa 3, il faut utiliser la définition de la tangente :
tan(/6)=[sin(/6)] / [cos(/6)] = 0,5 / (3 /2)

Posté par
christine1635slt patrice!! 19-05-07 à 16:25

merci pour ces info ca me facilite la tache!! tu es en kel classe?

Posté par
patrice rabillerre : Trigonometrie et fonction circulaire! 19-05-07 à 16:28

Je ne suis pas tout à fait d'accord avec les calculs de bruschetta1...

Personnellement je trouve :

\cos^2\frac{\pi}{12}=\frac{2+\sqrt 3}{4}

J'en déduis que : \sin^2\frac{\pi}{12}=\frac{2-\sqrt 3}{4}

Donc, puisque \sin\frac{\pi}{12}>0, \sin\frac{\pi}{12}=\sqrt{\frac{2-\sqrt 3}{4}}=\frac{\sqrt{2-\sqrt 3}}{2}

Posté par
christine1635a patrice!! 19-05-07 à 16:29

tu es en kel classe patrice??

Posté par
patrice rabillerre : Trigonometrie et fonction circulaire! 19-05-07 à 16:30

Il y a bien longtemps que je ne suis plus lycéen hélas ...

Posté par
christine1635a bruschetta 19-05-07 à 16:30

tu es en kel classe brushetta??

Posté par
bruschetta1re : Trigonometrie et fonction circulaire! 19-05-07 à 16:31

patrice tu as raison, je me suis rendu compte de mon erreur
6 = 6 et non 36
erreur d'inatention désolé

Posté par
bruschetta1re : Trigonometrie et fonction circulaire! 19-05-07 à 16:31

1ere

Posté par
christine1635a patrice!! 19-05-07 à 16:31

a bon!! t a la fac?? ta fé kel bac?? si je pose ces kestion c pour me rassurer et comparer les 2 reponse!!

Posté par
bruschetta1re : Trigonometrie et fonction circulaire! 19-05-07 à 16:32

6² = 6 et non 36 =)

Posté par
christine1635brushetta 19-05-07 à 16:33

j'avais aussi remarke cette erreur donc ca ma semble bizarre!! tu fé une premiere dans kel filier??

Posté par
bruschetta1re : Trigonometrie et fonction circulaire! 19-05-07 à 16:34

1ereS section SI

Posté par
christine1635a tt les 2!! 19-05-07 à 16:36

la ca me pose probleme puiske tt les 2 vs fait une bonne filiere!! mé vs mavé donner tt les 2 une reponse différente!! je ne sais plus laquelle choisir!! eske l'un de vous est totalement dakor sur sa reponse?? totalement sur??

Posté par
patrice rabillerre : Trigonometrie et fonction circulaire! 19-05-07 à 16:43

Pour vérifier si une réponse est bonne, il suffit de mettre ta calculatrice en mode radians, de calculer sin(/12), puis de comparer ce résultat avec les valeurs proposées ...

Ma calculatrice me dit que sin((/12)=0,9330127019...

Posté par
christine1635a patrice! 19-05-07 à 16:46

ok je vais suivre ton conseil!! enkor merci!! mé eske pr les deux autres exo tu as des idées? paske moi la jsui carement plante en + jsui stresse paske ca c les exos decisifs pour mon passage!!

tu ma tjr po di ten é ou ds t etude!!

Posté par
christine1635patrice 19-05-07 à 16:48

moi sin pi/12 me donne 0.2588190451...

Posté par
christine1635a brushetta!! 19-05-07 à 16:53

brushetta dou sor le 16 dans la 8eme ligne de ton calcul?

Posté par
christine1635re brushetta 19-05-07 à 16:57

tu pe me refaire aussi le calcul en rectifiant tes erreurs! dsl je c ke ca fé un pe chier mé jmen sor pa sinon

Posté par
bruschetta1re : Trigonometrie et fonction circulaire! 19-05-07 à 17:09

j'ai rectifié mon erreur et je trouve sinpi/12 = (8-2(12))/4
et j'en suis totalement sur

Posté par
christine1635brushetta 19-05-07 à 17:12

ca me rassure mé c a partir de kel ligne ke tu a fait cette erreur??

Posté par
patrice rabillerre : Trigonometrie et fonction circulaire! 19-05-07 à 17:13

C'est vrai je me suis trompé (ça arrive même aux profs ):

cos(/12)=0,9659258263...
sin(/12)=0,2588190451...

Sinon, pour les détails de calcul :

\cos\frac{\pi}{12}=\frac{\sqrt 6+\sqrt 2}{4}

donc \cos^2\frac{\pi}{12}=\(\frac{\sqrt 6+\sqrt 2}{4}\)^2=\frac{6+2\sqrt{12}+2}{16}=\frac{8+4\sqrt 3}{16}=\frac{2+\sqrt 3}{4}

donc \sin^2\frac{\pi}{12}=1-\cos^2\frac{\pi}{12}=1-\frac{2+\sqrt 3}{4}=\frac{4-2-\sqrt 3}{4}=\frac{2-\sqrt 3}{4}

Posté par
bruschetta1re : Trigonometrie et fonction circulaire! 19-05-07 à 17:13

la 3eme ligne j'ai ecrit 36+.......+4 , remplace 36 par 6 et 4 par 2

Posté par
christine1635re brushetta 19-05-07 à 17:13

je konfirm ke c bon je vien de verifier a la calculette!!

stp pour lexo 3 tu pe po m'aider?? depuis tt a leur je patauge sans trouver la reponse!

Posté par
christine1635a patrice!! 19-05-07 à 17:13

t prof???

Posté par
christine1635a vous 2!! 19-05-07 à 17:16

vous pouvez m'aider pour l'exo 3 aussi??
svp!!

Posté par
patrice rabillerre : Trigonometrie et fonction circulaire! 19-05-07 à 17:25

Oui ...

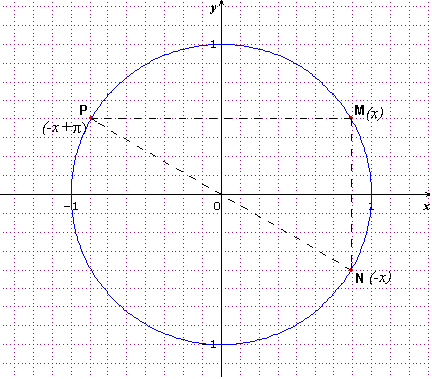
pour simplifier cos(-x-), il faut faire une figure.

Si on choisit un point M qui correspond à x, alors le point N qui correspond à -x est symétrique de M par rapport à l'axe des abscisses

Donc le point P qui correspond à -x- (ou à -x+) est symétrique de N par rapport à l'origine.

On peut remarquer que les projetés de P et de M sur l'axe des cosinus (Ox) sont opposés...

Trigonometrie et fonction circulaire!

Posté par
christine1635a patrice! 19-05-07 à 17:27

en fait jdoi juste faire un cercle avec les figures?? je n'ai pas de calculs a faire??

Posté par
patrice rabillerre : Trigonometrie et fonction circulaire! 19-05-07 à 22:05

En effet, ce genre de propriété se voit graphiquement et il n'est jamais demandé de les démontrer...


Rechercher
Menu
Espace membre
9 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !