Inscription / Connexion Nouveau Sujet
Trigonométrie - rectangle circonscrit au cercle
Soit une rectangle ABCD circonscrit au demi cercle de centre O et de rayon 2. Le point B du rectangle est circonscrit au cercle; Soit  l'angle formé par le segment [OB] et le diamètre.
l'angle formé par le segment [OB] et le diamètre.
Démontrer pour quelle valeur de  l'aire du rectangle sera maximale
l'aire du rectangle sera maximale
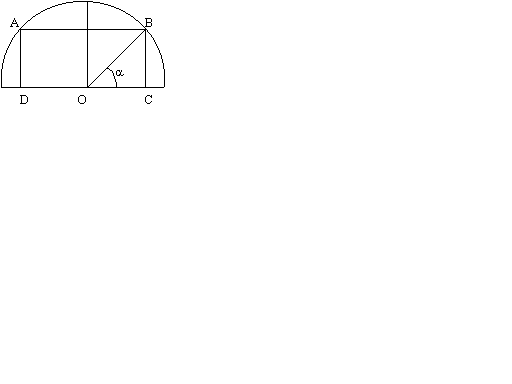
bonjour
il faut calculer les longueur 0C et CB
j appelle a=alpha
cos (a)=OC/2 OC=2*cos(a)
sin(a)=BC/2 BC=2*sin(a)
notons f l'aire du rectangle
f(a)=BC*2*OC=8*cos(a)*sin(a)
il faut etudier la fonction f et trouver son maximum
Merci pour le coup de main je trouve aussi Pi/4 en fonction par la fonction dérivée!


