Inscription / Connexion Nouveau Sujet
Trouver x
Bonjour, j?ai un petit souci avec mon exercice  voir la photo)
voir la photo)
Pour la question numéro une j?ai trouvé :
S(x)=(20-x)(20-x)
=(20-x)^2
=x^2-40x+400
Pour la question numéro deux j?ai trouvé :x^2-40x400>272
x^2-40x+128>0
Seulement voilà je ne sais pas comment trouver Le 2x^2
Pouvez-vous m?aider s?il vous plaît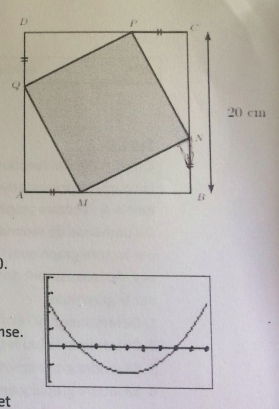
**image recadrée sur la figure**
bonjour
comme tu as bien lu les règles du forum ( ) avant de poster, tu as du voir que les images d'énoncé sont interdites...
) avant de poster, tu as du voir que les images d'énoncé sont interdites...
Bonjour,
si tu veux une réponse, tu dois te conformer à ![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
tu écris l'énoncé complet
tu postes les images des figures (ça on les a)
tu dis ce que tu as fait avec les numéros de question
Très bien je ferai donc cela .
Exercice :
Dans un carré a BCD de côté 20 cm on inscrit un carré MNPQ suivant le schéma ci-contre (voir la photo )
On pose x=AM=BN=CP=DQ avec 0<_ x<_20.
Le but de cet exercice et de déterminer les valeurs de X pour lesquelles l'air du carré MNPQdépasse 272 centimètres
carrés .
1. Calculer l'aire du carré MNPQ en fonction de X . Cette terre exprimés en centimètres carrée sera noté s(x) et sera donnée sous la forme développée est réduite .
Réponse:
S(x)=(20-x)(20-x)
=(20-x)^2
= x^2-40x+400
2. Prouver que l'inéquation S(x)>272 Équivaut à 2x^2-4x+128>0
Réponse :
X ^2-40x+400>272
X^2-40x+128>0
Seulement voilà je n'arrive pas à trouver le 2X^2
De Plus je n'arrive pas à faire la question numéro trois qui est la suivante
3. On donne ci-contre la représentation graphique de la fonction X —>2x^2-40x+128 sur l'intervalle [0;20]
( voir la photo )
l'aire demandée est le carré d'un de ses côtés... S(x)=MN² par exemple
tu as tout sur la figure pour calculer MN²
Je viens de me corriger et je pense que la réponse est la suivante :
Pour trouver la longueur du côté et MN il faut utiliser le théorème de Pythagore :
MN^2=MB^2+NB^2
=(20-x)^2+x^2
=2x^2-40x+400
Elle se trouve dans le message où j'ai rédiger l'exercice .
Ceci dit je peux vous la réécrire
3. On donne ci-contre la représentation graphique de la fonction X —>2x^2-40x+128 sur l'intervalle [0;20]
( voir la photo )
Oui excusez moi j'ai oublié d'écrire le reste. La suite de la question est donc la suivante :
Conjecturer l'ensemble des sous lussions du problème en expliquant la réponse
ben si on appelle f cette fonction du cherche à résoudre f(x)>0 ...
on te demande une résolution graphique là
En réalité je n'ai pas trop bien compris comment faut-il procéder ?
J'avais déjà compris qu'il fallait faire une résolution graphique mais je ne sais pas comment faire avec cette exercice
tu cherches les valeurs de x (abscisse) telles que f(x) (ordonnée du point de la courbe d'abscisse x) soit positif...
Je viens d'effectuer l'exercice et je pense que la réponse est la suivante :
0;2;4;16;18;20
L'ensemble des solutions du problème sont les suivantes car X doit être positive en effet dans l'exercice il est écrit 0<_x<_20
Bien sûr je le sais mais dans ce cas il serait mieux que je fasse des intervalles. Car il y aurait beaucoup trop de solution


