Bonjour,

La curiosité n'est pas un défaut, bien au contraire

Les nombres d'un triangle de Pascal sont des nombres entiers.  Il peuvent se calculer de proche en proche ou bien en utilisant la fonction "factorielle".

Par exemple, pour calculer factorielle(5), qui s'écrit 5! , on fait :

5!=54321
Par convention on pose 0!=1

Le début de ton triangle de Pascal doit ressembler à ceci :

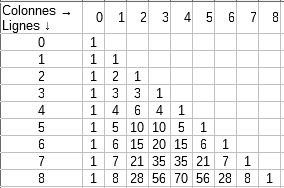
Pour calculer les nombres qui se trouvent dans la colonne 3, par exemple il faut écrire :

Ces nombres ne sont définis que pour n3 (parce qu'on veut calculer les nombres de la colonne 3).

Ainsi, par exemple,

Je connaisais déjà les factorielles, et je te le confirme, la curiosité n'est pas un defaut, en tout cas, je fais relire ton commentaire jusqu'a que je comprennent ! Mais merci beaucoup

En faite, c'était très facile a comprendre ! As-tu une explications mathematiques pour ce calcul ? J'aimerais comprendre pourquoi ce calcul marche

Les nombres de la forme , avec n et p entiers et pn, sont très utilisés pour les dénombrements (calculs de probabilités par exemple).

Ce nombre s'appelle "nombre de combinaisons de p objets choisis parmi n".
Par exemple, on choisit 5 cartes dans un jeu de 32 cartes. Quel est le nombre de "mains" possibles ? C'est, tout simplement , soit 201376.

Les calculatrices disposent de fonctions toutes faites pour ces calculs...

La démonstration de ce résultat est un peu compliquée. On peut utiliser par exemple un raisonnement par récurrence. Je ne suis pas sûr de pouvoir te l'expliquer clairement (ces démonstrations ne sont pas au programme des classes de lycée)... mais tu dois trouver facilement des démonstrations détaillées sur internet

Wow, ça à l'air compliqué, ducoup je vais aller voir sur internet

Merci beaucoup de m'avoir aider !