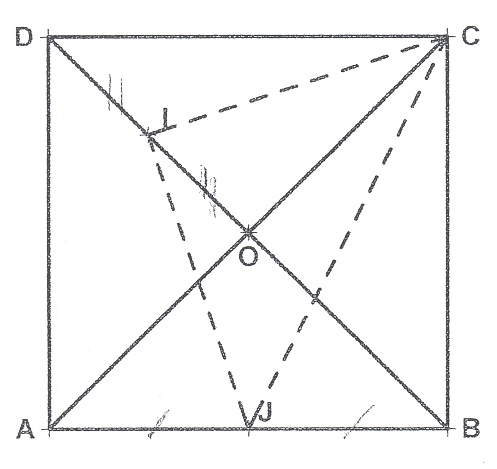
Bonjour ,

en te plaçant dans le repère (AB , AD)  trouve les coordonnées des points I , J et C  pour déterminer les longueurs des segments IJ et IC . Tu peux aussi faire avec Pythagore .
Ensuite , tu peux écrire l'équation des droites IJ  et  IC  pour voir si elles ne seraient pas orthogonales .
Tu peux aussi pour cela te contenter de Pythagore .

Cordialement

Bonjour,
Le triangle CIJ semble rectangle isocèle.
Pour le démontrer, tu peux essayer de calculer les longueurs des côtés.
CJ facile avec Pythagore. CI peut aussi se trouver avec Pythagore. Pour IJ , c'est peut-être un peu plus compliqué.
Il n'est pas impossible qu'une autre démonstration plus simple existe

Bonjour, merci pour vos idées de réponse mais c comment on calculer les coordonnées que je ne comprend pas.
Pouvez vous plus détaillé svp
Merci d'avance.

Bonjour,

Une méthode sans Pythagore...

1) Soit c le côté du carré. CI et IJ sont tous deux l'hypoténuse de triangles rectangles (à tracer) dont les côtés de l'angle droit mesurent c/4 et 3c/4. CI et IJ sont donc de même longueur.

Donc le triangle CIJ est isocèle de sommet I.

2) Soit alpha la mesure de l'angle de la "pointe" d'un triangle rectangle dont les côtés de l'angle droit sont dans un rapport 1/2.

L'angle ICJ mesure alpha + (45 - alpha) = 45°

Donc le triangle CIJ est donc rectangle isocèle de sommet I.

Cela reste à rédiger proprement, bien sûr.

Nicolas

Merci Nicolas_75, ta méthode 1 à l'aire bien mais pourrais tu dévelopé stp je sais que je te demande beaucoup mais je beug vraiment sur cet exercice.
merci de m'aider

Je détaille un peu l'utilisation de Pythagore :
JC est la longueur de l'hypoténuse d'un triangle rectangle. Les autres côtés ont pour longueurs 1/2 et 1 .
De même pour IC avec IO et OC . la diagonale du carré a pour longueur 2 . On en déduit facilement les longueurs IO et OC .

Pour la longueur IJ, on peut tracer la parallèle à (AD) issue du point I . Elle coupe (AB) en H et (CD) en K. D'après Thalès, HB = 3/4 et IH = 3/4 ; donc HJ = 1/4 . Utiliser ensuite le triangle rectangle IJH .

Remarque : Comme Nicolas_75 l'explique, la longueur IC peut se trouver aussi avec le triangle rectangle ICK, ce qui montre que le triangle CIJ est isocèle en I et évite des calculs avec 2.

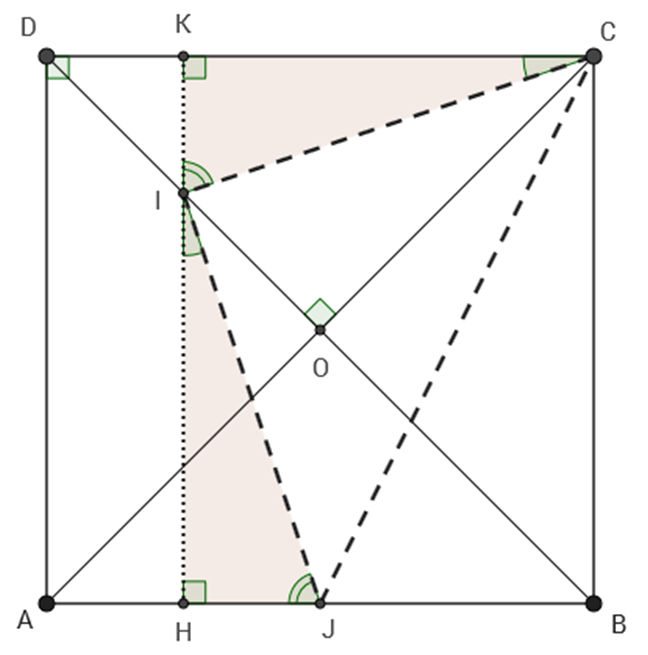
J'ai essayé de simplifier encore ma méthode. Cf. figure ci-dessous.

Soit c la longueur du côté du carré ABCD.

Soit K et H les projetés orthogonaux de I sur (CD) et (AB).

Les triangles CKI et IHJ sont égaux / superposables / isométriques.

En effet,
a) le théorème de Thalès permet de montrer que CK = IH = 3c/4 ;
b) le théorème de Thalès permet de montrer que KI = HJ = c/4 ;
c) les angles CKI et IHK sont droits.

La première conséquence est que les troisièmes côtés sont égaux : CI = IJ, donc le triangle CIJ est isocèle de sommet I.

Deuxième conséquence de cette égalité des triangles...

En décomposant l'angle plat :
CIJ = 180° - KIC - HIJ
Or l'égalité des deux triangles impose que HIJ = KCI, donc :
CIJ = 180° - KIC - KCI
Or, au sein du triangle rectangle KIC, KIC + KCI = 90°, donc :
CIJ = 180° - 90°
CIJ = 90°

Donc le triangle CIJ est un triangle rectangle en I.

En conclusion, le triangle CIJ est isocèle rectangle de sommet I.

Nicolas

Merci beaucoup Nicolas_75 j'ai très bien compris les deux parties, mais pouvez-vous m'expliquer le a), b) et c) svp
merci énormément d'avance

Par exemple, pour calculer la longueur IH, tu peux appliquer le théorème de Thalès dans la configuration B, I, D / B, H, A.

Désolé mais je ne vois pas très bien
D'avance merci

Applique le théorème de Thalès dans le triangle BAD avec les points intermédiaires I et H : tu pourras en déduire la longueur IH.

???
Merci d'avance

Je ne comprends pas ton dernier message, posté seulement 2 minutes après le mien. Je doute que tu as eu le temps de faire quoi que ce soit.
Applique le théorème de Thalès dans le triangle BAD : qu'obtiens-tu ?

Mais c comment les longueur que je ne connais pas
D'avance merci

Montre tes calculs...

Ba je n'est pas de calcul car je ne sais pas comment connaître les longueurs
Peut tu m'expliquer
Stp

Stp

Cela ne sert à rien de faire des exercices si tu ne connais pas ton cours.
Révise ton cours sur le théorème de Thalès.
Applique-le dans le triangle BAD.

Bonjours, j'ai un DM à faire mais je ne sait pas comment démontrer que le triangle CKI
est égale au triangle IHJ
Merci d'avance pour votre aide



*** message déplacé ***

Multipost avec https://www.ilemaths.net/sujet-trouver-la-nature-d-un-triangle-655111.html

*** message déplacé ***

Bonsoir, I est sur la diagonale donc IC = IA mais IA = IJ puisque H a l'air d'être au milieu de AJ. donc IJ = IC
les deux triangles ont donc leur hypoténuse égale. Si en plus ils sont un angle respectivement égal (ils en ont même deux sur la figure) alors c'est un cas d'égalité des triangles, ils sont égaux.

*** message déplacé ***

ha zut je n'avais pas vu que c'était un multipost grrr ...

*** message déplacé ***

Désolé pour se multipost je ne voulais pas en faire un mais je ne comprenais vraiment pas

*** message déplacé ***