Inscription / Connexion Nouveau Sujet
Trouver longueur segment
Bonjour,
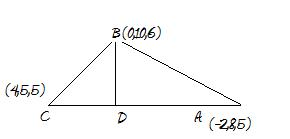
Je ne sais pas si je me trouve dans le bon niveau de scolarité puisque je suis québecoise, j'étudie niveau cegep en mathématique : algèbre vectorielle et linéaire, géométrie. Mais, je pose la question quand même. Voici mon problème, je dois trouver la longueur du segment AD. Dans le triangle les segments BD et AC sont perpendiculaires.
Malheureusement, je ne sais pas par ou commencer. Je sais que les segments BD et AC étant parallèle cela fait en sorte quils forment un angle de 90 degré dans les deux côté du triangle.
Merci à l'avance pour votre aide.
Lily_J
Bonjour,
Puisque et que
et
sont colinéaires, on peut écrire :
où k est un réel
Si on pose D(x,y,z) on doit pouvoir trouver facilement les coordonnées de D (surtout qu'on peut remarquer tout de suite que z=5) 
Petites questions :
1)AC * BD = 0
2) AD = k AC
Comment on fait pour passer de 1) a 2)?
Et pourquoi ecrire k ?
Merci !!!
Bonjour
Si tu as vu le produit scalaire :
tu calcules le produit scalaire
de 2 façons différentes
1) en utilisant le produit de AC par la longueur du projeté orthogonal de AB sur AC
2) en utilisant les données sur le triangle ABC
soit les 3 longueurs de côté sont données
soit les coordonnées des 3 points sont données
Bonjour,
Je sais comment trouver le produit, mais je ne suis pas sur de comprendre à quoi cela ca servir ?
Merci
Bonjour,
J'ai essayé quelque chose et j'aimerais savoir si c'est bon :
D = C + vecteur CD
OD = OC + vecteur CD
= OC + vecteur CB projette sur vecteur CA
= OC + vecteur CB *vecteur CA/ ||CA||^2 * vecteur CA
= (4,5,5) + (0,10,6)*(-6,3,0)/||(-6,3,0)||^2 * (-6,3,0)
= (4,5,5) + (0+30+0)/ racine de 45 * (-6,3,0)
= (4-180/racine de 45, 5+90/racine de 45,5)
Voilà!!!
Est-ce que mon raisonnement semble bon et ma réponse par le fait même ???
Merci à l'avance!
Je ne comprends pas ta réponse...
Si on part de A(-2;8;5), B(0;10;6) C(4;5;5) et D(x;y;z)
Alors on a ;
et
Donc l'égalité équivaut à 6x-3(y-10)=0 (1)
L'égalité : équivaut à
(2)
En utilisant l'équation (1) et le système (2) on arrive à
Connaissant les coordonnées du point D, on peut maintenant calculer la distance AD (je trouve )
sauf erreur 
Rebonjour,
En utilisant l'équation (1) et le système (2), comment tu fais pour arriver à cette réponse???
Merci
D'ou vient AD = k AC, quest-ce qui te permet d'affirmer cette égalité???
Les points A,B,C sont alignés. Donc les vecteurs
Le système (2) vient directement de l'équation
Salut,
J'ai compris les équation 1 et 2 et quelles valeurs tu as pris.
Ce que je ne comprend pas cest que tu as utilisé l'équation 1 et le système 2. Ce que je veux savoir cest comment tu as fait pour arriver a la réponse. Serait-ce possible pour toi de me l'écrire, du moins juste le début?
Merci
Je reprends à partir de l'équation (1) 6x-3y+30=0 et du système (2) :
ou, plu simlement :
De la seconde équation du système, je déduis : 3k=-y+8 donc 6k=-2y+16
Je remplace, dans la première équation du système, 6k par -2y+16. Cette première équation devient : x+2=-2y+16
En joignant cette équation avec l'équation (1), j'obtiens un système de deux équations à deux inconnues :
Il est facile de trouver x et y. Par ailleurs on sait que z=5 (3è équation du système (2) )
Voilà ... 


