Inscription / Connexion Nouveau Sujet
trouver une fonction a partir de ses asymptotes
Trouver l'expréssion d'une fonction f décroissante sur chacun des intervalles où elle est définie et dont la courbe représentative admet deux asymptotes d'équation x=-2 et y =3.
donc si j'ai bien comrpi on doit trouvé une fonction dont la limite = 3 quand x tend vers + et dont la limite =-2 quand x tend vers 0
et dont la limite =-2 quand x tend vers 0
mais a part sa je ne vois pas du tout comment trouver la fonction
pouvez vous m'aider ?
donc si j'ai bien comrpi on doit trouvé une fonction dont la limite = 3 quand x tend vers +

Oui.
et dont la limite =-2 quand x tend vers 0
Non.
Si une fonction f admet une asymptote d'équation x=a, cela signifie que :


Maintenant, pour trouver cette fameuse fonction, on va s'aider d'une fonction connue, que tu peux trouver facilement 
Connais-tu une fonction décroissante sur les intervalles où elle est définie, tendant vers une limite finie, et admettant une asymptote verticale, c'est-à-dire une asymptote d'équation du type x=a avec des limites (quand x tend vers a) + ou -  ?
?
bonjour
Au minimum :
x=-2 asymptote => P(x)/(x+2)
y=3 asymptote => P(x)=3x+k
il faut déterminer k pour que la dérivée soit négative
(tu devrais trouver k>6)
Sauf erreur
Rudy
Voilà, 1/x était la fonction que je voulais que tu trouves.
Seulement, l'asymptote horizontale est en 0, et la limite en + est 0.
est 0.
Il faut donc décaler 1/x de 3 unités vers le haut pour avoir une asymptote horizontale d'équation y=3 en + . Soit g(x) = (1/x) + 3.
. Soit g(x) = (1/x) + 3.
Il reste maintenant le problème de l'asymptote verticale à régler. On veut en quelque sorte "décaler" la fonction g de 2 unités vers la gauche, pour décaler l'asymptote en x=-2.
Ainsi, f(x) = g(x+2) = (1/(x+2)) + 3
Si tu n'as pas compris quelque chose (ce qui est fort probable vu mes explications  ), fais le savoir, j'essaierai de t'expliquer un peu mieux
), fais le savoir, j'essaierai de t'expliquer un peu mieux 
Pour finir, voici un petit grpah :
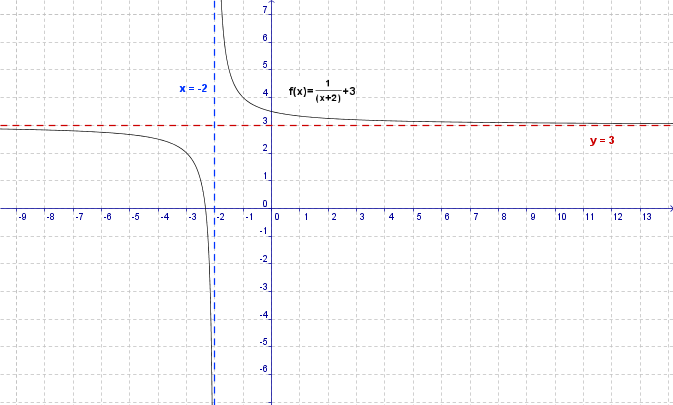
Note bien que la fonction n'est pas la seule à répondre aux critères.
Toutes les fonctions du type avec n impair correspondent aussi

Je fais un bref retour sur la notion des décalages verticaux et horizontaux d'une fonction :
-Soit f une fonction. Pour décaler f verticalement de a unités vers le haut, il suffit d'ajouter a à f.
ex : f(x) = x² Je veux créer g(x), la fonction f(x) décalée de 3 unités vers le haut, g(x) = x²+3
Inversement, si on veut décaler de a unités vers le bas, il faut retrancher a à f 
-Soit f une fonction. Pour décaler f horizontalement de a unités vers la gauche, il suffit d'ajouter a à la variable que prend f en entrée (c'est pas clair, c'est normal  )
)
ex : f(x) = x² Je veux créer g(x), la fonction f(x) décalée de 3 unités vers la gauche, g(x) = (x+3)²
Si on veut décaler vers la droite, on retranche.
ex : f(x) = x² Je veux créer g(x), la fonction f(x) décalée de 3 unités vers la droite, g(x) = (x-3)²
Excuse-moi si je n'emploie pas les termes adéquats, mais l'essentiel c'est de comprendre 



