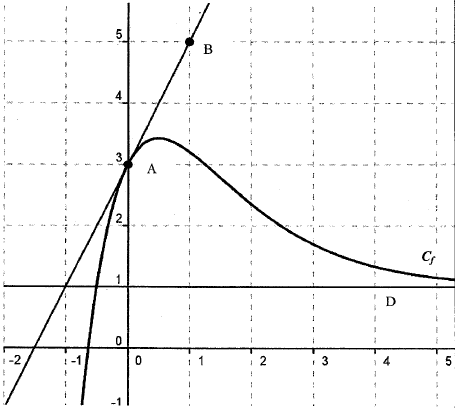
L'unité d'aire, c'est l'aire d'un carré 1 X 1, tout simplement.
Dans un devoir, on peut te demander une aire "en unités d'aire" ou "en cm²"
Si ton graphique a pour échelle 2 cm pour une unité d'abscisse  et 2 cm pour une unité d'ordonnée alors une unité d'aire vaut 4 cm².  Si on te demande "en unité d'aire" tu te contente de compter les carrés de 1 X 1 !

bonjour,
ton "énoncé" si l'on peut dire n'est pas très clair!
Donne le nous (complet)

Il n'y aurait les intégrales dans l'air ?????

je retire quelque part ce que j'ai écrit.
pythamede que je salue m'a éclairé sur le questionnement de Jonasjo

L'énoncé est le suivant:
"Préciser un encadrement par deux entiers consécutifs de l'aire, en unités
d'aire, de la partie du plan située entre la courbe Cf , l'axe des abscisses, l'axe
des ordonnées et la droite d'équation x = 1."

Je ne comprends toujours pas malgré les explications de pythamede. Je ne vois aucun lien logique avec l'aire d'un carré. Puissez vous reformuler. Merci

Bonjour

l'unité d'aire est l'aire du rectangle formé à partir des vecteurs de base ,
on a donc

si vous coloriez le domaine ainsi défini  vous verrez que vous coloriez  trois carrés complets + une certaine surface

on peut donc bien dire que l'aire de ce domaine est compris entre 3 et 4 unités d'aire  puisqu'on n'a pas sa transcription en

Bonjour,

Tout d'abord , tu dois comprendre ce que veut dire une unité d'aire !! C'est une définition dont tu dois connaître.
Ceci est d'ailleurs très bien par notre ami pythamede, c'est l'aire d'un carré 1x1.
Une fois que tu as compris cela, passons à ta question :

bonjour ,

comprends-tu ce que veut dire "unité de longueur" ou pas ???
parce que le fond du problème est là et nulle part ailleurs.

une fois que tu as compris (réellement compris) ce que veut dire unité de longueur
que tu as compris (réellement compris) ce que veut dire le mot "aire", que deux figures géométriques différentes peuvent avoir la même aire etc
la définition de l'unité d'aire est : l'aire d'un carré de côté égal à l'unité de longueur

et si on te demande de dire que l'aire d'un patatoïde est comprise entre 3 et 4 unités d'aire, cela veut dire que l'aire de ce patatoïde est égale à entre 3 et 4 fois celle d'un carré de côté égal à l'unité de longueur

et c'est tout.

quant au rapport avec ton exo c'est ça :

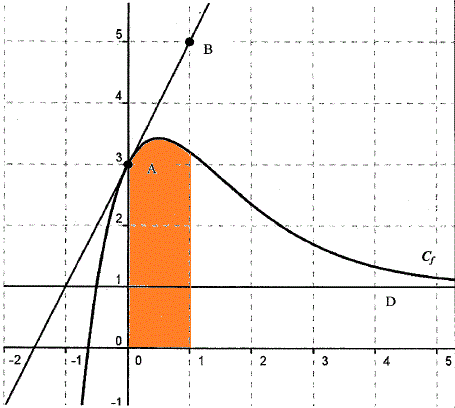
on te demande d'estimer l'aire de la partie orange en "carreaux"
unité d'aire = aire d'un carreau = celle d'un carré de côté l'unité de longueur (l'unité de longueur est celle qui est marquée "1" sur les axes)
la réponse est totalement évidente graphiquement, non ?
cela ne nécessite aucune dissertation de pages entières sur la signification du mot "unité d'aire"

elle se justifie formellement en prouvant que dans [0; 1] f(x) >= 3 (donc aire > 1*3, aire d'un rectangle de 1 unité de largeur sur 3 unités de hauteur)

et que la courbe est au dessous de sa tangente, donc l'aire est inférieure à celle du trapèze déterminé par cette tangente
c'est à dire 1*(3+5)/2