Inscription / Connexion Nouveau Sujet
Un petit problème
Bonsoir, j'ai besoin de votre aide pour un exercice que je ne comprends pas.
Voici ce que l'énoncé dit :
le carré ABCD , ci-contre a un côté de longueur 8 cm . M est un point pris au hasard sur le segment [AB] . On construit , a l'intérieur , le carrée de côté [AM] et le triangle rectangle isocèle d'hypoténuse [MB].On s'intéresse aux aires du petit carré , du triangle et du motif constitué par le carré et triangle.
1) Donner l'aire Ac du carré en fonction de x.
2) Montrer que l'aire At du triangle en fonction de x est
(4-(x/2)²
3) Donner l'aire Am du motif en fonction de x.
4) Est-il possible de faire en sorte que
a) l'aire du motif soit de 40 cm²?
b) L'aire du triangle soit égale à l'aire du carré ?
c) L'aire du motif soit la plus petite possible ?
5)Donner les solutions exactes (ou à défaut une approximation) de chacun de ces trois problèmes.
L'aire du carré est x² (ça c'est facile) mais je ne comprends pas l'aire de la question 2.
voici la figure :
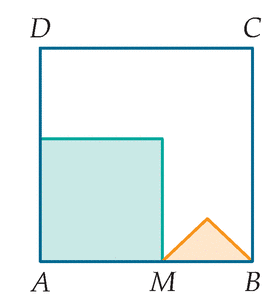
Un exercice que tu "ne comprends pas " . . . .
Tu dois pourtant bien savoir calculer l'aire d'un carré ou d'un triangle !
Je dis que je ne comprends pas car l'aire du triangle rectangle isocèle aurait été (x/2)2 si un de ses côtés était le segment [AM] mais ce n'est pas le cas alors je ne comprends l'equation. ;~;
C'est (MB] qui forme un côté du triangle rectangle, et non [AM] .
Que trouves-tu pour l'aire de ce triangle en fonction de x ?
2) Cette expression donne bien l'aire du triangle en fonction de x . Reste à modifier son écriture pour parvenir à l'expression de l'énoncé.
Par ailleurs, j'ai deviné que x était la longueur du segment [AM].
Bonjour
Montrer que l'aire At du triangle en fonction de x est
(4-(x/2)²
en recopiant correctement l'énoncé cela serait plus clair!!
vu qu'il manque visiblement une parenthèse, reste à savoir où elle est ...
et il ne doit pas y avoir place à la divination.
Bonjour dumby
Priam a écrit
Par ailleurs, j'ai deviné que x était la longueur du segment [AM].
dans un énoncé recopié correctement tout doit être écrit, il n'est pas question de jouer aux devinettes....peut-être que si tu avais lu le point 3 de



