Bonjour, voilà j'ai un problème à faire pour lundi, j'ai aucune idée de la solition, donc si vous pouviez m'aider:

Problème: Une ville carrée de dimensions inconnues possède une porte au milieu de chacun de ses cotés.
Un arbre se trouve à 20 pas de la porte Nord, à l'exterieur de la ville. Il est visible d'un point que l'on atteint 14 pas vers le sud à partir de la porte Sud, puis 1775 pas vers l'ouest. Quelle est la dimension de chaque côté?

Merci d'avance.

*** message déplacé ***

édit Océane : merci de ne pas poster ton exercice dans des topics différents, les rappels sont pourtant bien visibles.
En postant un petit message dans ton topic, il remonte automatiquement parmi les premiers.

Multi-Post Un problème chinois

*** message déplacé ***

Bonjour,

Il me semble que j'ai déjà vu cet énoncé sur un autre forum ; essaye avec un moteur de recherche et les mots :

ville arbre porte nord pas forum

ou toute autre combinaison des mots de ton énoncé  

Il a été traité plusieurs fois ici  ...

Pour trouver les topics concernés, il faut utiliser la fonction Recherche représentée par une loupe dans le cadre en haut à droite, avec le mot

ville arbre porte nord pas forum

Bonne recherche !

bonsoir,


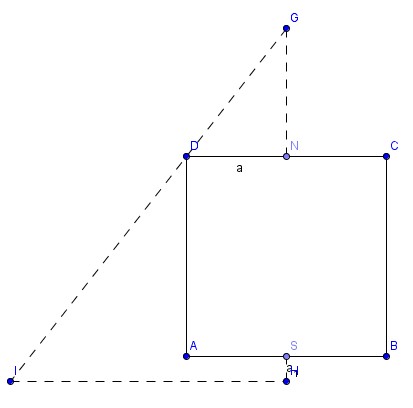
Voici un essai pour obtenir un résultat. Voir la figure et quelques indications

G="arbre" N="Nord"    S="Sud"      NG=20 pas   , SH=14 pas   HI=1775 pas et le côté du carré vaut 2a...
En pointillés le chemin parcouru...

Je suppose que du point I on frôle le sommet D du carré et on voit l'arbre en G...

Ecrivons que tan(GIH) = tan(GDC)

Le segment GH = 20+2a+14=34+2a

tan(GIH)=(34+2a)/1775

tan((GDC) = 20/a



D'où l'équation (34+2a)/1775 = 20/a

soit a(34+2a) =20*1775

2a²+34-20*1775=0

a²+17-17750=0   équation du second degré en a

=71289=(267)²

d'où la solution positive a=125 pas

d'où le côté du carré 2a=250 pas



bon dimanche...