Inscription / Connexion Nouveau Sujet
Un triangle mobile
Voici l'énoncé :
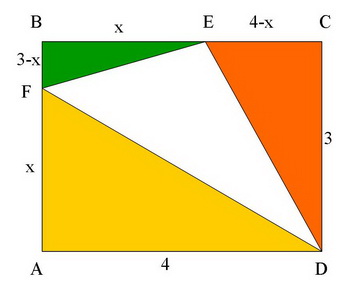
Dans un rectangle ABCD tel que AB=3 et AD=4, on construit un triangle comme sur la figure ci-dessous. Le point E se déplace sur [BC] et on a AF=BE.
1.a. La construction est-elle possible pour toutes les positions de E sur [BC]? Justifier.
1.b. Réaliser la figure à l'aide d'un logiciel de géométrie dynamique et conjecturer l'ensemble des positions de E telles que l'aire de EFD soit supérieure où égale a 4,2.
2. On appelle A(x) l'aire de EFD en fonction de la longueur x de BE.
2.a. Quel est l'ensemble de définition de A?
2.b. Exprimer A(x) en fonction de x.
2.c. Démontrer que, pour tout x de l'ensemble de définition, A(x)=1/2(x-2)² + 4.
3. Démontrer la conjecture.
3.a. En utilisant les variations de A.
3.b. En réalisant un tableau de signes.
J'ai réussi toutes les questions sauf la 3 ème, pouvez-vous m'aider 🙂
la FAQ du forum
Où en êtes vous exactement ?
2 b calcul de l'aire l'avez-vous effectué ? aire totale - aires des triangles colorés
2 c développez le résultat donné ou trinôme du second degré
3 a grâce à la forme précédente établir le sens de variation minimum ?
3b résolvez ou après transformation
factorisation, signe des différents facteurs , tableau, conclusion
un fichier pour étudier les variations 
Fonction polynôme de degré 2 et parabole
Pour le sens de variation, vous avez peut-être vu que si a>0 alors la fonction est décroissante sur et croissante sur
le minimum vaut alors obtenu en
ou le sommet de la parabole est le point de coordonnées
Bonjour
vous avez montré que pour on a donc une valeur
pour laquelle
pour il existe donc une valeur
pour laquelle
l'aire du triangle DEF=4,2 lorsque
on ne peut pas être plus précis à moins de prendre la table d'une calculatrice pour obtenir une valeur approchée
on aura les valeurs exactes en résolvant
Annuler
connectez vous