Inscription / Connexion Nouveau Sujet
Une formule de duplication
Bonjour à tous,
J'ai un devoir maison à faire en mathématiques, et je ne sais vraiment pas par où commencer mon exercice. Voici le sujet :
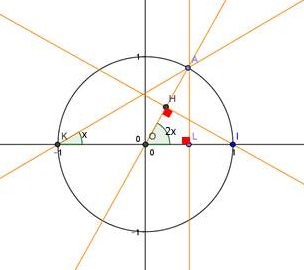
On considère le cercle trigonométrique associé au repère orthonormé direct (O,I,J), et le point K de coordonnées (-1;0) et un réel x.
On place sur le cercle le point A tel que (KI,KA) = x. Le but de ce problème est de démontrer l'égalité : sin2x = 2sinxcosx
1) on suppose dans cette question que x  [0;
[0; /2]. La perpendiculaire à [OA] passant par I coupe la droite (OA) en H.
/2]. La perpendiculaire à [OA] passant par I coupe la droite (OA) en H.
a) démontrer que (OI,OA) = 2x
b) démontrer que sin2x = IH
c) démontrer que l'aire du triangle rectangle AKI est égale à 2sinx cosx
d) démontrer que les triangles AKO et AOI ont la même aire égale à IH/2
2) on suppose dans cette question que x [
[ /2;
/2; ]. On pose x' = x -
]. On pose x' = x -  /2
/2
a) démontrer que : sin2x' = 2sinx' cosx'
b) en déduire que l'on a encore : sin2x = 2sinx cosx
3) on suppose dans cette question que x [-
[- ;0] et on pose x'' = -x
;0] et on pose x'' = -x
a) démontrer que : sin2x'' = 2sinx'' cosx''
b) en déduire que l'on a encore sin2x = 2sinx cosx. On a ainsi démontré que cette égalité est vraie pour tout réel x de l'intervalle [- ;
; ]
]
4) démonter que pour tout réel x, on a :
Sin2x = 2sinx cosx
Bonjour,
As tu commencer par faire un dessin? (ça aide pas mal quelque fois, même souvent, voire toujours)
Pour t'aider à démarrer:
OK et OA sont 2 rayon du cercle trogi. Donc le triangle KOA est isocèle.
Comme l'angle (OKA) vaut x, le fait que le triangle KOA soit isocèle te dit que l'angle (KAO) vaut également x.
Et donc l'angle (KOA) vaut  -2x, et l'angle (IOA) vaut alors 2x.
-2x, et l'angle (IOA) vaut alors 2x.
C'est bon, la fusée est allumée?
N'hésite pas si ça bloque un peu plus loin
Bonjour,
Merci beaucoup pour votre aide pour cette première question, elle est complètement triviale. Cette question était très simple....
Pourriez-vous me dire comment vous feriez pour la question b). Sans me donner les réponses, simplement une piste .
Merci d'avance 
Re-
Je ne qualifierai pas la question 1) de triviale ... déjà 1 + 1 = 2 n'a rien de trivial alors les propriété des triangles isocèles ...
Donc pour b)
Tu dois remarque que le triangle OHI est rectangle en H et OI est son hypoténuse de longueur 1
Une formule de trigo de fin de 3eme doit revenir à ta mémoire.
Euh ...
L'énoncé est plutôt sympa en te précisant que le triangle AKI est rectangle ... en A d'ailleurs (mais ça tu peux admettre que ton correcteur est disposé à l'admettre ...)
Comme tu sais que:
- l'angle (IKA) vaut x
- et que IK = 2 (diamètre du cercle trigo)
L'application de la même formule de trigo qu'au b) te donne la réponse!
Je viens de trouver la réponse.
L'exercice n'est pas pour demain, je m'arrête là pour ce soir. Si jamais j'ai besoin de votre aide demain en début de soirée, serez-vous toujours disponible ?
Merci en tout cas pour l'aide que vous m'avez déjà fournie 
J'essaierai de tout laisser tomber pour répondre ... 
Pour avoir jeter un œil à la suite je crois que si tu a "vaincu" le 1)c) tu as fait le plus dur.
Après on the demande d'appliquer des règles de trigonométrie qui doivent se trouver sur ton bouquin de cours.
Je me permets d"ajouter une question à l'énoncé:
le raisonnement que nous avons fait ne porte que sur [0, /2] visiblement, puisque l'objet des questions 2) et 3) est de prouver la même égalité sur [
/2] visiblement, puisque l'objet des questions 2) et 3) est de prouver la même égalité sur [ /2;
/2; ] puis sur [0;-
] puis sur [0;- ]
]
Ma question donc: à quel moment dans notre raisonnement avons nous fait une hypothèse telle que le périmètre de validité s'en est retrouvé réduit à [0, /2]
/2]
Rien à gagner ... si ce n'est ma considération bien sûr 
A+
Pour répondre à votre question, il est vrai qu'à aucun moment nous ne faisons entrer en jeu ce domaine réduit, mais est-ce vraiment utile ? Ce n'est qu'une supposition...
Une dernière petite question et je vous laisse tranquille pour ce soir, pour la question d), je trouve l'aire du triangle AOI qui est bien IH/2, mais je n'arrive pas à montrer que celle-ci est égale à l'aire du triangle AKO.
Je ne vous demande pas une réponse dès ce soir, votre vie est plus importante que mon exercice de maths.
Je vous dis peut-être à demain,
Bonne soirée, et merci beaucoup 
il est vrai qu'à aucun moment nous ne faisons entrer en jeu ce domaine réduit
Si tel était le cas ... les question 2) et 3) n'auraient pas de sens ne crois tu pas.
En fait, dans la question 1 le fait que x
 [0;
[0; /2] est utilisé implicitement à 2 moments en b) et en d) où il est nécessaire que H soit à l'intérieur du segment [O;A] à moins d'utiliser des formules du type sin(
/2] est utilisé implicitement à 2 moments en b) et en d) où il est nécessaire que H soit à l'intérieur du segment [O;A] à moins d'utiliser des formules du type sin( -2x) = sin(2x) ce que l'on veut éviter parce admettre celle ci reviendrait à admettre le résultat ...)
-2x) = sin(2x) ce que l'on veut éviter parce admettre celle ci reviendrait à admettre le résultat ...)Oui, je comprend ce que vous voulez dire. Mais tel que nous avons traité les questions, elles sont justes, n'est-ce pas ?
Je reste bloquée à la question d). J'arrive à montrer que l'aire du triangle AOI vaut IH/2, mais je ne vois pas comment faire pour montrer que cette même aire est égale à celle du triangle AKO. Auriez-vous une idée ? 
Je viens de trouver la réponse à la question d).
J'ai oublié de mettre une question qui est 1)e) conclure.
Je pense que je dois en conclure la formule sin2x = 2sinxcosx ?
Super! (pour la question 1)d) ...)
Effectivement pour conclure sur 1)e)
tu dis
aire de AKI = aire AKO + aire AOI = 2 fois IH/2
Et donc tu as la relation trigonométrique établie ...
2) et 3) devraient être de simples formalités ... ou pas?
On reste vigilant 
Voilà ce que je trouve pour la question e), dites moi ce que vous en pensez :
Aire de AKO + aire de AOI = aire de AKI
IH/2 + IH/2 = 2sinxcosx
2IH/2 = 2sinxcosx
IH = 2sinxcosx
Sin2x = 2sinxcosx
Il valait mieux être vigilant !
Je coince un peut pour commencer la question 2)...
Je me sens nulle.....
J'ai la réponse 3) en entier, mais pour la question 2), je trouve un - d'un côté mais pas de l'autre... Avez-vous une idée ?
Pour la question 4) pour démontrer pour tout réel x, cela suffit si je dis que dans les questions précédentes, x prend de certaines valeurs ?
Je viens de me rendre compte que ce devoir est pour demain....
Merci d'avance
Vous devez certainement vous dire que je fais un monologue, mais je viens de trouver la solution aux dernières questions. Avec le temps, les réponses viennent toutes seules, mais il faut tout de même réfléchir.
Je vous remercie de votre aide, vous m'avez beaucoup apporté, je pense que sans vous, je n'aurais pas pu commencer l'exercice.
Au plaisir de "retravailler" avec vous si jamais j'en ai besoin.
Je vous souhaite encore une bonne fin de soirée,
A+
Désolé, j'étais occupé ...
Pour 2), si x  [
[ /2 ;
/2 ;  ] alors x'
] alors x'  [0 ;
[0 ;  /2]
/2]
et comme x' = x -  /2
/2
sin2x' = 2sinx'cosx' d'après 1) avec par ailleurs
sinx' = -cosx
et
cosx' = sinx
2x' = 2x - 
donc
sin2x' = - sin2x
En remplacant dans la formule sin2x' = 2sinx'cosx'
tu arrives (tu es arrivé!!!) à
sin2x = 2sinxcosx
Raisonnement du même genre pour 3)
Quand on sait que sinx'' = -sinx et cosx'' = cosx
Pour le 4) tourner de 2k ne change pas les valeurs de cos et de sin ...
ne change pas les valeurs de cos et de sin ...
Bon, au plaisir, n'hésite pas si questions
coucou 
j'ai besoin d'un petit coup de pouce, en ce qui concerne ce même exo,
je bloque pour la question 2)a) malgré des essaies en vain.
si vous avez des idées, avec plaisir
Bonjour
Ce que je suggérais (et que je suggère toujours) c'est d'utiliser les propriétés suivantes:
On a donc , donc
si , alors
On peut donc appliquer à x' le résultat de 1)
soit
Et donc en utilisant les propriétés rappelées plus haut
On a bien le résultat demandé: et
salut,
merci de l'aide, mais y'a un truc qui me gène pourquoi
vous avez : si x'= x-Pi/2 , alors x' appartient a (0; Pi /2 ) ?
je croit que c'est sa qui me géne vraiment, parce que les formules je l'es ai et puis de
la qst 1) e) j'arrive a la conclusion suivant : sin 2x = 2 sinxcosx
aaa j'allais oublié comment faite vous pour l'aire de AKO ?
Merci de l'aide
Ps: Kimylepetit, non je ne suis pas en 1er 8
Eh ben ... C est souvent les memes exo qui reviennent en DM dailleurs.
Même question pour l'auteur. 1re 8 ?
Bonjour à tout le monde,
Tout d'abord une petite précision: dans la question 1) la démonstration de sin2x = 2 cosxsinx, n'est faite que pour x  [0;
[0; /2]
/2]
Le pourquoi de cette limitation est expliqué dans le message du 2/5 à 9h20.
Donc si on veut démontrer que ceci est vrai  x
x 
 , il faut encore le démontrer sur le reste de l'intervalle [
, il faut encore le démontrer sur le reste de l'intervalle [ /2 ; 2
/2 ; 2 ]
]
On se pose donc la question sur [ /2 ;
/2 ;  ] (question 2) puis sur [
] (question 2) puis sur [ ; 2
; 2 ] (question 3).
] (question 3).
Pour revenir maintenant aux demandes d'éclaircissement:
vous avez : si x'= x-Pi/2 , alors x' appartient a (0; Pi /2 ) ?
Dans la question 2) on prend x
 [
[ /2 ;
/2 ;  ] (c'est l'énoncé qui le dit) et si
] (c'est l'énoncé qui le dit) et si
x
 [
[ /2;
/2;  ]
]
alors en prenant x' = x -
 /2,
/2,
x'
 [0;
[0; /2]
/2]
(si Z compris entre 10 et 20, Z' = Z - 3 sera compris entre 7 et 17)
Et donc on peut appliquer à x' la propriété trouvée au 1)
aaa j'allais oublié comment faite vous pour l'aire de AKO ?
Je fais comme je peux ... mais j'aurais pas du jeter mon papier

AKO a pour base 2cosx et pour hauteur sinx donc AKO = sinxcosx
de même AOI à pour base AO = 1 et pour hauteur HI
La conclusion est proche!
Est plus clair?
Re coucou,
alors vous allez rigoler mais sérieux je sui sperdu ,
j'ai malgré tous du mal a retomber sur ce qu'il me dise ?
pour l'aire de AKO je doit mettre en évidence IH, du coup de comprend pas
pourquoi de doit utiliser cos ?
Ne te laisse pas perturber par l'énoncé
si tu préfères ne pas utiliser les sinus et cosinus apparents  mais introduire un nouveau point tu arrives encore plus vite au résultat
mais introduire un nouveau point tu arrives encore plus vite au résultat
Soit donc L l'intersection de (KI) et de sa perpendiculaire passant par A:
Donc
Mais [HI] est aussi une hauteur de AOI
donc
On est bon comme cela?
Je bloque à la question 1 c.
Demontrer que l'aire de AKI est égale à
Je trouve un autre résultat ...
Je trouve ça.
Donc Aire de AKI =
Et non pas 2 sin x cos x comme on est sensé trouver ... Ou est mon erreur ? :s
presque... que représente L ?
la 2) a) je voit toujours pas comment aboutir au résultat 
Merci, dsl de te donner du travail en ce samedi.
alors
sin x = AI/2
cos x = AK/2
oublie pas que KI est un diametre du cercle, donc = 2
voila avec sa c'est bon ?
sin x = AI/2
cox x = AK/2
donc 2sinxcosx= 2*Ai/2*AK/2 ( un 2 se sup )
tu retrouve bien la même formule que AK*AI/2
c'est vrai que j'ai pris le pb a l'envers mais je pense que sa tient la route
tu vois ?
donc 2sinxcosx= 2*Ai/2*AK/2 ( un 2 se sup )
Tu le sors d'ou ce x2 ?
Je ne saisi pas comment vous en arrivez là.
En fait vu que on fait
Il faudrait trouver
Et c'est donc ce
2cosx*2sinx/2 = 2sinx*cos x parce que tu as un 2 en bas et 2 en haut, tu peut simplifier ?
parcontre si qq1 peut prendre le temps de me re expliquer la 2) sa serai sympa
Re-,
Je laisse Doudou177 gérer les questions de KimiLePitit ... bon moyen de vérifier qu'il/elle a bien crompris 
Je reviens aux 2 questions posées par Doudou177
que représente L
L est l'intersection entre la droite (IJ) et la perpendiculaire à A passant par (IJ)
autrement dit, L représente l'abscisse de A dans le repère (O,I,J)
Autre question plus dérangeante
la 2) a) je voit toujours pas comment aboutir au résultat
Je suis désespéré ... un dernier essai
soit x dans l'intervalle [
 /2 ;
/2 ;  ]
]
Si on définit un autre réel, que l'on appelle x' et qui vaudra x' = x-
 /2
/2
Es tu d'accord que comme x
 [
[ /2 ;
/2 ;  ]on a x'
]on a x'  [0;
[0;  /2]
/2]
Si tu es d'accord avec cela, alors tu peux appliquer à x' les résultats du 1)
sin2x' = 2sinx'cosx'
On est toujours bon où tu bloques déjà?
Si tu es d'accord avec cela tu appliques les formules de trigo énoncées plus haut (si elles ne sont pas évidentes pour toi, fais un dessin)
On refais un point quand on est calé jusque là!
Ahhh, aide moi s'il te plait, justement, je ne comprends pas ce que veux me dire doudou ou bien il/elle se trompe lors de sa factorisation 
Ce serait bien que je débloque de là pour enchainer au deux, là ensuite, je pourrai rejoindre votre conversation 
Alors je croit avoir compris, mais le truc c'est que j'arrive pas au résultat voulut...
PerArGal t'es un ange de vouloir m'expliquer,
je croit que si j'arrive à cette qst je reussirai les autres...
bon,
je reprends de là où tu bloques
On est d'accord sur
C'est toi qui l'a écrit à 16h29 aujourd'hui
donc
On est bon?
@doudou177
mais le truc c'est que j'arrive pas au résultat voulut...
Sois plus précis STP, peux tu détailler ton raisonnement? et le résultat auquel tu arrives?
Courage! on y est presque ... ou ........pas?
d'accord j'essaye
AKI = AOI + AKO
AKI = IH/2 + IH/2
AKI = 2IH/2
2sinxcoxs = IH
2sinxcoxs = sin 2x
c'est sa ou pas du tous ? pour la conclusion de e) ?
PerArGal,
tu n'aurai une autre manière de prouver que AKO = IH/2
parce que j'ai fait ta facon plusieur fois mais non je voit pas.
Pour AKI :
je fais b*h/2 soit AO*HI/2 = HI/2
comment est ce que cela pourrait être autre chose? et en plus cela te permet d'arriver au résultat. Cependant, ce résultat, je croyais que tu l'avais acquis!
Mhh, oui j'arrive à cela, merci.
Pour la 1)d.
J'arrive à montrer que
Mais je n'y arrive pas avec le triangle AKO. Une piste ? :s
J'ai lu ta méthode qui revient à dire que AL est une hauteur de AKO ... Mais je ne vois pas en quoi ça en est une en fait ..
C'est bon pour la 3). J'ai trouvé.
La 4), je sais comment faire mais ... De quel manière dois-je la rédiger ?
Merci beaucoup pour votre aide.
Il me reste donc l aire du triangle AKO que je n'arrive pas à démontrer.
Je m excuse pour ce quadriple post.
Bonjour,
On essaie de se le terminer aujourd'hui cet exercice? En parcourant les derniers échanges, je vois 2 points en suspens 1) calcul de l'aire de AKO et 2) rédaction de la réponse à la question 4 ... Si d'autres sujets se sont "rouverts" pendant la nuit, n'hésitez pas ...
1) Aire de AKO (à l'aide de la figure jointe)
Première méthode: en introduisant le point L
L étant l'intersection entre (KI) et la perpendiculaire à (KI) passant par A
Donc [AL] est une hauteur du triangle AKO
or KO = 1, donc
(eq. 1)
Passons au triangle AOI
On a maintenant 2 hauteurs pour ce triangle HI (base OA) et AL (base OI)
donc
Or OA = OI = 1, donc
(eq. 2)
En reprenant les équations eq. 1 et eq. 2 en une seule:
Deuxième méthode utilisant sinus et cosinus:
AKO est isocèle en O, donc
Base AK = 2KO.cos(x) (avec KO = 1)
Hauteur = 1/2.AK.sin(x)
Aire de AKO = cos(x).sin(x) = 1/2.Aire de AKI
Et comme Aire de AKI = Aire de AKO + Aire de AOI, on a aussi AOI = sin(x).cos(x) = 1/2.HI (1/2 base x hauteur)
2) rédaction de démonstration du 4)
Je ne sais pas comment votre cours définit la congruence modulo 2 et je n'ai pas de bouquin sous la main. On va essayer de faire le plus simple possible
et je n'ai pas de bouquin sous la main. On va essayer de faire le plus simple possible
Soit x un réel quelconque:
La division euclidienne de x par (2 ) fournit un entier k et un réel r tels que
) fournit un entier k et un réel r tels que
x = 2 .k + r avec r
.k + r avec r [0;2
[0;2 [
[
Or on sait que:
Nous avons tout ce qu'il faut pour répondre maintenant:
Soit x un réel quelconque:
 (k,r)
(k,r) 
 x
x , tels que
, tels que
x = 2k + r avec r
+ r avec r [0;2
[0;2 [
[
Donc
(eq. 1)
et
(eq. 2)
Or r  [0;2
[0;2 [, donc r vérifie
[, donc r vérifie
(eq.3)
La combinaison de (eq. 1), (eq. 2) et (eq.3) nous donne bien:
C'est bon? 
Et en plus j'ai une bonne nouvelle, vous allez bientôt ajouter à votre formulaire de trigo à savoir par cœur sans besoin de justifier:
cos(a+b) = cos(a)cos(b) - sin(a)sin(b)
sin(a+b) = cos(a)sin(b) + sin(a)cos(b)