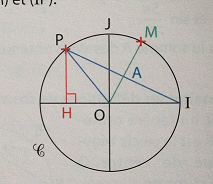
(O;I;J) est un repère orthonormé et C est le cerlcle trigonométrique de centr O.
x désigne un réel de l'intervalle ]0;π/2[, M est le point de C associé à x, et P celui associé à 2x.
H est le ponit de l'axe des abscisses tel que le triangle PHI soit rectangle en H et A le point d'intersection des droites (OM) et (IP)

1.a) Quelle est la nature du triangle IOP?
b) Démontrer que les droites (OM) et (IP) sont perpendiculaires et que A est le milieu de [IP]
2.Démontrer que :
-OA=cos x
-IA=sin x
-PH= sin 2x
3. En calculant de deux façons différentes l'aire du triangle OIP, démontrer la formule de duplication du sinus : Sin2x=2sinx cosx

Bonjour ,le 1.a) est réalisable, mais la suite est incompréhensible. Si qualqu'un pourrait me donner quelque explication se serait gentil. Un grand merci aux sauveurs.