Inscription / Connexion Nouveau Sujet
Utiliser la convexité
Bonjour, pourriez-vous m'aider s'il vous plaît à faire cette exercice :
Le nombre de pains produits à l'heure dans une entreprise, en dizaine de milliers, en fonction du nombre n de travailleurs employés, en centaine d'employés, vérifie P(n) = 3/8 n^2 - 1/32 n^3.
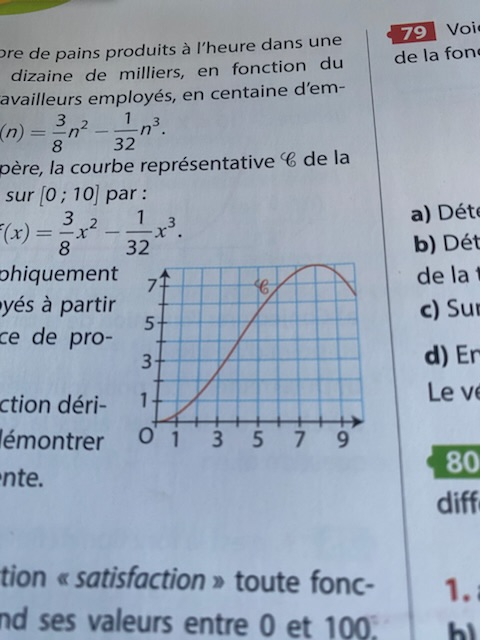
Voici, dans un repère, la courbe représentative c de la fonction f définie sur [0;10] par :
f(x) = 3/8 x^2 - 1/32 x^3.
a) Conjecturer graphiquement le nombre d'employés à partir duquel la croissance de production diminue .
b) Déterminer la fonction dérivée seconde de f et démontrer la conjecture précédente .
Merci d'avance de votre aide .
Pour commencer , la a) je pense que graphiquement le nombre d'employés à partir duquel la croissance de production diminue c'est 8. Mais je suis vraiment pas sûr . Corriger moi si c'est faux s'il vous plaît .
Bonjour
Vous avez donné le maximum de pains produits
ce n'est donc pas un ralentissement de la croissance
La deuxième question aurait dû vous guider.
On cherche à partir de combien d'employés la croissance diminue, c'est donc à partir de combien la pente des tangentes diminue.
Oui désolé vous avez raison je pense que graphiquement c'est à partir de 9 employés que la croissance diminue
Bonjour,
Je réponds en l'absence hekla et m'éclipserai quand il reviendra.
La fonction représentée semble atteindre un maximum égal à 8 pour n = 8.
Mais il faut bien lire l'énoncé :
nombre n de travailleurs employés, en centaine d'employés,
Moi aussi, je n'ai pas bien lu l'énoncé 
Il ne s'agit pas de voir quand la production diminue.
Mais quand elle croit moins vite.
Dans ce but, en partant de l'origine du repère, il faut regarder quand la courbe semble cesser d'être convexe.
Désolé du retard j'avais pas vu le message. La courbe semble cessait d'être convexe à 5 donc 500 employés ?
J'aurais plutôt dit 4 et 400. Mais bon...
En fait, rajouter du "environ" permet sans doute de retomber sur ses pieds au b).
Pour le b), qu'as-tu fait ?
Pour la b) f'(x) = 2x-3x^2
f''(x) = 2-6x après pour démontrer la conjecture je ne sais pas comment on fait .
Il faut des parenthèses autour des fractions quand elles sont écrites "en ligne" :
f(x) = (3/8) x^2 - (1/32) x^3
Que sont devenus 3/8 et 1/32 dans ton calcul de dérivée ?
(3/8) x^2 = 3/8 x 2x = 6/8 x - (1/32) x^3 = 1/32 x 3x^2 = 3/32x ^2
f'(x) = 6/8x - 3/32x^2
Est ce que f'(x) est bon s'il vous plaît ?
Votre écriture est un peu bizarre.
x est une lettre
est le symbole de la multiplication On le trouve dans
à défaut *
Désolé c'est une erreur de frappe .
Et f seconde c'est :
f''(x) = 3/4 - 3/32  2x
2x
f'´(x) = 3/4 - 6/32x
f''(x) = 3/4 - 3/16x
Est ce que c'est bon s'il vous plaît ?
C'est bien ce que vous avez écrit
J'indiquai simplement un chemin plus rapide pour le coefficient de .
Non, il faut résoudre l'inéquation qui peut se ramener
16 >0 on peut multiplier les deux membres par 16 on obtient alors
on peut ensuite mettre 3 en facteur
Je suis désolé mais j'ai vraiment pas compris comment vous faites l'inéquation, s'il vous plaît réexpliquer moi
À résoudre
Façon brute
On regroupe les termes en x dans un membre, les termes constants dans un autre
On multiplie les deux membres par l'inverse de soit
Comme le nombre est négatif, cela renverse le sens de l'inégalité.
et on simplifie
un peu moins brute
en mettant
en facteur puis en divisant les deux membres par
on obtient d'où
Non, le nombre d'employés à partir duquel la croissance de production diminue est de 400 employés.
La dérivée seconde est positive entre 0 et 4, donc la fonction est convexe sur
Elle est négative à partir de 4, donc la fonction est concave.
De rien Pourquoi un féminin ?


