D'ailleurs dans mon cahier de vacances ils me mettent :
On les classe par famille : la famille des /2, des /3, des /4 et des /6...mais ils ne développent pas et dise d'aller voir dans la chapitre n°8 de Method's machin, que je n'ai pas ^^'

Merci pour votre aide !

Déjà, tu sais que

Ensuite, pour les , tu sais que c'est du 0 ou du 1...

Pour , c'est pas trop compliqué non plus, c'est 2/2 pour le cos et le sin.

Pour et  , c'est pareil pour cos et sin, mais inversé...

De pauvres moyens mnémotechniques...

Mais faut les connaître, ça aide pas mal !

merci beaucoup ! =) Je galère beaucoup beaucoup avec la trigonométrie c'est horrible ! Trop de mal à comprendre -_- ayant eu une prof que ne savais pas expliquer le pourquoi et le comment, je recherche les cours de seconde dans les livre et internet, mais c'est moins facile à comprendre qu'avec un bon prof qui a ses méthodes ! =)
Merci encore , bon après midi sous le soleil !

il y a quand même une technique pour retenir facilement ces valeurs remarquables. c'est simplement classé sous un ordre croissant :

-cos(/2) = (0)/2      (=0)
-cos(/3) = (1)/2      (=1/2)
-cos(/4) = (2)/2      
-cos(/6) = (3)/2
-cos(0)       =   (4)/2     (=1)

en gros a chaque fois tu rajoute 1 a l'intérieur de la racine. Pour sinus, c'est la meme chose, sauf que c'est dans l'autre sens. Pour tangente, y'a juste a faire le calcul. Mais bon, c'est une technique qui sert juste au début car au bout d'un moment, a force d'utiliser ces valeurs, tu les retiendras comme ça.

Merci beaucoup, mais en faite ils me mettent par exemple : cos (2/3) = (sin 5/6) vrai ou faux...la réponse je l'ai dans les corrigés, mais je ne sais pas comment la trouver assez rapidement avec leur méthode de famille...j'ai donc comander leurs livre "Méthode'S Seconde" pour pouvoir mieux comprendre.
Merci !

en faisant un cercle trigonometrique, ca doit etre plus facile.

method'S c'est un livre que je recommande à tous le monde.

Oki Aizen, merci ! =)
Oui je recommande aussi Methode'S (en tout cas le cahier de vacance), c'est remplis d'humour, et de clin d'oeils..ça fais plaisir de faire des maths en rigolant un peu =D
Par contre, il y a beaucoup de fautes dans la correction je trouve -_-, un peu moins bien ça...

Bonjour!
J'essaye moi aussi de comprendre un peu la trigo.
Et j'ai moi aussi un cahier, et je n'arrive pas du tout a comprendre l'histoire des familles.
Par contre, je comprends le tableau de base
"cos(/2) = (0)/2      (=0)
-cos(/3) = (1)/2      (=1/2)
-cos(/4) = (2)/2      
-cos(/6) = (3)/2
-cos(0)       =   (4)/2     (=1)
"
Mais je ne comprends pas ce qu'il se passe quand on rajoute des nombres au numérateur.
Merci d'avance..

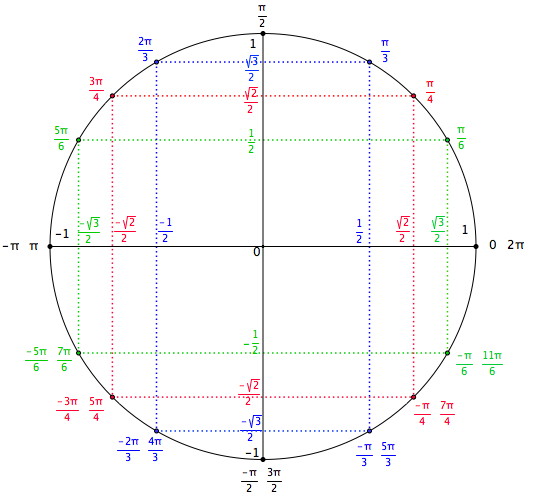
Bonjour,
ci dessous une image du cercle trigonométrique.
Propriétés à savoir :
1) quand deux angles sont complémentaires alors Sin (de l'un) = Cos (de l'autre)
Rappel : deux angles complémentaires ont pour somme l'angle droit (/2 en radian)
si x et y sont complémentaires x + y = /2 donc y = (/2) - x et par conséquent
Sin[(/2) - x] = Cos x et
Sin x = Cos[(/2) - x]

Par exemple /3 + /6= (2*)/6 + /6 = (3)/6 = /2 don
Sin (/3) = Cos(/6) et
Cos(/3) = Sin(/6)

2) quand ddeux angles sont supplémentaires ils ont le même Sin et des Cos opposés
Rappel : deux angles supplémentaires ont pour somme l'angle plat ( en radian)
Si x et y sont supplémentaires alors x + y = et y = - x et par conséquent
Sin( - x) = Sin x et
Cos(-x) = -Cos x

3) quand deux angles sont opposés ils ont même Cos et des Sin opposés
Sin( -x) = - Sin x et
Cos(-x) = Cos x

Sur le cercles trigonométrique :
des angles complémentaires correspondent à des points symétriques par rapport à la 1 ^ère bissectrice
des angles supplémentaires correspondent à des points symétriqques par rapport à l'axes des ordonnées
des angles opposés correspondent à des points symétriques par raport à l'axe des abscisses.

Quand on te renvoie à la famille des /2, /3, /4,... je crois (mais je n'en suis pas certain) qu'il s'agit des familles suivantes :
famille des /3 : /3, (2)/3, (3)/3, etc....
même chose pour les autres familles...

J'espère que ces quelques renseignements t'aideront....

Alors là, vraiment MERCI Tilk_11 !
C'est beaucoup plus clair pour moi!!!
Vraiment Merci beaucoup!
Mais alors, pour reprendre ce qui est dit plus haut, pour cos(2/3) = sin(5/6) , d'après le cercle on voit bien que (sin 5/6)= sin (/6 ) . Et on voit aussi bien que cos(2/3)= -cos(/3)
Mais comment justifier ca par la calcul ? Ou en seconde on ne demande qur faire graphiquement?
Mais c'est le seul "probleme" qui me reste.
Merci encore Tilk_11, je me repette, mais ca m'a été d'une grande aide!!

*** " on voit bien que cos(2/3)= cos(/3)
[ je ne voulais pas mettre le "-" ]  "

tu as bien fais d'écrire que
Cos (2/3)= - Cos (/3) car c'est juste
en effet 2/3 et /3 sont supplémentaires puisque
2/3 + /3 =
Pour ce qui est de ta question
/6 et 5/6 sont aussi supplémentaires donc ils ont le même Sin donc
Sin(5/6 = Sin (/6 = (3)/2
d'autre part
Cos (2/3)= - Cos (/3) = -(3)/2
donc tu peux en déduire que
Cos (2/3)= -Sin(5/6

Ok !
Merci beaucoup!!
Donc la seule justification c'est qu'il faut c'est qu'ils soient supplémentaires ou complémentaires?
Ou je peux tout de suite dire que
Sin(5/6 = Sin (/6) ?
Et encore Merci !

Bonjour,
si on te demande une justification tu peux expliquer de la façon suivante :

"Les angles 5/6 et /6 sont supplémentaires en effet 5/6 + /6 = 6/6 = ,
or
"Quand deux angles sont supplémentaires, ils ont le même Sin"
donc
Sin 5/6 = Sin /6."
Est-ce que cela répond à ta question ?

Bonjour!
Oui merci, c'est ce que je voulais savoir.
La trigonometrie prends un autre sens quand on comprend
Vraiment je te remercie, parcequ'en plus d'avoir compris ce que j'ai vu en 2nde,j'ai appris d'autre chose,comme le règlé sur les angles supplémantaires par exemple.
Vraiment merci beaucoup beaucoup !!
Bonne  Journée!

Bonne journée à toi aussi...
@ + peut-être

Bonjour !!
Je ne comprends pas la partie de la trigonométrie dans mon bouquin de méthode avec les angles -x, -x, +x, /2+x... les angles associés à x quoi... ce que je ne comprends pas c'est comment déterminé leurs cosinus et sinus en fonction de cos(x) et sin(x)....
J'ai le cercle et toute les formules, ils disent que c'est le la lecture graphique, mais je ne comprends pas leurs lecture.
Ce n'est pas très clair désolée, mais si quelqu'un comprends ce que je veux dire et veux bien m'aider je lui en serais très reconnaissante =D
Merci d'avance et bonne soirée !

Personne n'a de conseils pour comprendre ?

Bonjour,

Le cercle trigonométrique que Tilk_11 a joint en image est issu d'un forum où on explique comment le lire et le retrouver : c'est ici

Si tu as des questions tu peux toujours les poser.

Merci Bourricot, et bonne soirée