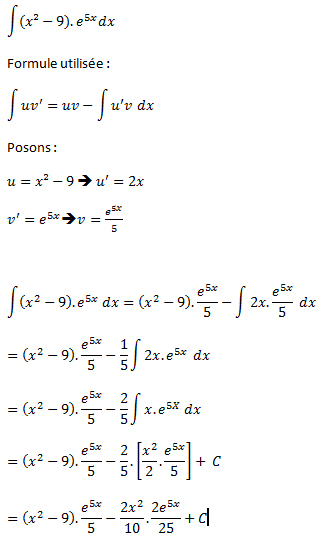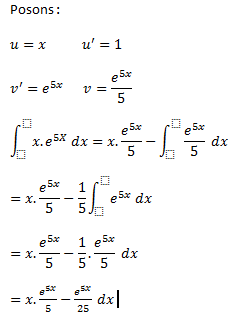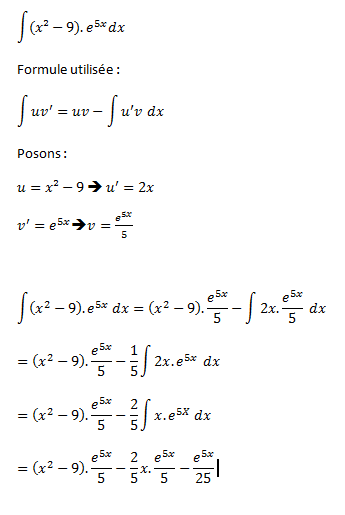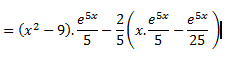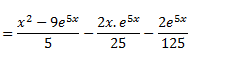Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale IntégrationTopics traitant de Intégration [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Vérification calcul intégrale

Posté par
zap21 17-06-10 à 14:10

Bonjour,

Je passe mon examen de mathématique demain et je m'entraine à refaire quelques intégrales. Cependant, je n'arrive pas à vérifier mes réponses et j'ai toujours de gros doute quant à leur exactitude. Pouvez vous m'aider s'il vous plaît ?

1. (x-3).(x+3).e5xdx

Ma réponse ==>(x²-9).e5x/5 - x²/5 . 2e5x/25 + C

Après simplification, j'obtiens ceci ==> 5x²-45.e5x - x² . 2e5x/5 + C


Je tiens à signaler que je suis absolument pas sûr de ma réponse, donc soyez indulgents

Merci d'avance

Posté par
jacqlouisre : Vérification calcul intégrale 17-06-10 à 14:20

    Bonjour .  Un moyen bien simple pour vérifier son résultat :
        --->   tu dérives  ta réponse !...
et tu dois retrouver l'expression sous l'intégrale .

Posté par
cailloux Correcteurre : Vérification calcul intégrale 17-06-10 à 14:24

Bonjour,

Pour contrôle, une primitive de ta fonction est F définie par:

F(x)=\left(\frac{x^2}{5}-\frac{2}{25}x-\frac{223}{225}\right)\,e^{5x}



Posté par
cailloux Correcteurre : Vérification calcul intégrale 17-06-10 à 14:26

Evidemment une fôte:

F(x)=\left(\frac{x^2}{5}-\frac{2}{25}x-\frac{223}{125}\right)\,e^{5x}

Posté par
Camélia Correcteurre : Vérification calcul intégrale 17-06-10 à 14:29

Bonjour

Le plus simple pour vérifier une primitive est de la dériver...

Je ne trouve pas comme toi... (mais je fais aussi souvent des erreurs de calcul)

\Large\bigint(x^2-9)e^{5x}dx=\frac{(x^2-9)e^{5x}}{5}-\bigint\frac{2xe^{5x}}{5}dx=\frac{(x^2-9)e^{5x}}{5}-\frac{2xe^{5x}}{25}+\bigint_\frac{2e^{5x}}{25}dx=\frac{(x^2-9)e^{5x}}{5}-\frac{2xe^{5x}}{25}+\frac{2e^{5x}}{125}+C

et en dérivant on a l'air de tomber sur la formule de départ!

Posté par
Camélia Correcteurre : Vérification calcul intégrale 17-06-10 à 14:29

Bonjour à tous! 223?

Posté par
cailloux Correcteurre : Vérification calcul intégrale 17-06-10 à 14:32

Bonjour Camélia,

Oui, oui:

-\frac{9}{5}+\frac{2}{125}=\frac{223}{125}

Posté par
Camélia Correcteurre : Vérification calcul intégrale 17-06-10 à 14:33

Oh, yes! J'en reviens pas... je l'avais juste!

Posté par
cailloux Correcteurre : Vérification calcul intégrale 17-06-10 à 14:34

Posté par
cailloux Correcteurre : Vérification calcul intégrale 17-06-10 à 14:35

Sauf que moi j' ai encore faux: c' est \frac{223}{125} avec un signe +!

Alors que tout est écrit correctement sur mon brouillon...

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 14:37

Bonjour,
On cherche une primitive de:
4$ f:x \to (x^2-9) \times e^{5x}
Calculons alors:
4$ F(x)=\bigint_a^x f(t)dt=\bigint_a^x (t^2-9) \times e^{5t}dt=\bigint_a^x t^2e^{5t}dt-9\bigint_a^x e^{5t}dt=I(x)-\frac{9e^{5x}}{5}+C
En faisant une intégration par parties pour I(x):
4$ I(x)=\bigint_a^x t^2e^{5t}dt=\frac{x^2e^{5x}}{5}+C-\frac{2}{5}\bigint_a^x te^{5t}dt=\frac{x^2e^{5x}}{5}+C-J(x)
En faisant une intégration par parties pour J(x):
4$ J(x)=\frac{2}{5}\bigint_a^x te^{5t}dt=\frac{2}{5}(\frac{xe^{5x}}{5}+C-\bigint_a^x \frac{e^{5t}}{5}dt)
Donc:
4$ J(x)=\frac{2}{5}(\frac{xe^{5x}}{5}-\frac{e^{5x}}{25}+C)
Ainsi:
4$ I(x)=\frac{x^2e^{5x}}{5}+C-J(x)=\frac{x^2e^{5x}}{5}-\frac{2xe^{5x}}{25}+\frac{2e^{5x}}{125}+C
Donc:
4$ F(x)=I(x)-\frac{9e^{5x}}{5}+C=\frac{x^2e^{5x}}{5}-\frac{2xe^{5x}}{25}-\frac{223e^{5x}}{125}+C


Les primitives de f sont donc de la forme:
4$ F(x)=\frac{x^2e^{5x}}{5}-\frac{2xe^{5x}}{25}-\frac{223e^{5x}}{125}+C

Posté par
cailloux Correcteurre : Vérification calcul intégrale 17-06-10 à 14:37

Rhôôô! non c' était finalement bien écrit avec un signe -

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 14:37

Ouah... j'arrive après la guerre là...

Posté par
cailloux Correcteurre : Vérification calcul intégrale 17-06-10 à 14:39

Oui mais c' est bô!

Bonjour thiblepri

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 14:40

Salut cailloux
Bon au moins c'est -223

Posté par
Camélia Correcteurre : Vérification calcul intégrale 17-06-10 à 14:44

Salut thiblepri (moins en retard que l'autre jour...)

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 14:45

Et que tout à l'heure ... Non mais je te dis je suis en mode archéologie sur l'île des maths ; y'a des sujets intéressants

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 14:51

Je suis complètement pomé. Je ne vois pas comment arriver à cette réponse.

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 14:56

@ zap21: que ne comprends-tu pas dans mon post?

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 15:00

Attends, je vais te mettre tout mon développement et tu me diras où ça coince, ca sera plus simple. Déjà on ne fait que des intégrations par partie, et on note x, pas t :p C'est un peu perturbant. Je te mets mon développement dans 2 minutes.

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 15:12



Vérification calcul intégrale

Posté par
Camélia Correcteurre : Vérification calcul intégrale 17-06-10 à 15:20

Ca coince à la fin... Comment passes-tu de \bigint xe^{5x}dx à la suite? Il faut recommencer une intégration par parties...

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 15:20

Tu te trompes au passage de l'avant avant dernière ligne à l'avant dernière.
x->x*e^5x n'admet pas x->x^2*e^5x pour primitive

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 15:22

Je dois reposer ? Comment je sais lorsque je dois reposer ? Quand il n'y a plus de x ?

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 15:23

Lorsque tu ne connais pas de primitive, tu peux essayer par intégration par parties

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 15:25

Je reposte la suite alors, dés que je l'ai fais. Laissez moi 2 minutes.

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 15:38

La suite

Vérification calcul intégrale

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 15:41

Très bien (sauf que tu as laissé des dx), maintenant tu intègres ça dans ce que tu avais trouvé précédemment.

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 15:46

Mais je n'arrive pas à tout regrouper, comment dois-je m'y prendre ?

Vérification calcul intégrale

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 15:52

Tu oublies des parenthèses à la fin.

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 15:55

Comme ça ?

Vérification calcul intégrale

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 15:56

Voilà, tu développes et tu devrais retrouver ce qu'on a trouvé

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 16:09

C'est ça ?

Vérification calcul intégrale

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 16:12

Oui, mais tu peux encore réduire l'expression.

Posté par
zap21re : Vérification calcul intégrale 17-06-10 à 16:22

Je sais pas du tout comment continuer :s Peux-tu m'indiquer la marche à suivre étape par étape ?

Posté par
thibleprire : Vérification calcul intégrale 17-06-10 à 17:03

Tu mets tout au même dénominateur

Posté par
trivisteamisre : Vérification calcul intégrale 17-06-10 à 17:23

Salut les gars,

Bon je vais vous mettre tous d'accord, je trouve :

\int(x-3)(x+3)e^{5x}=\frac{1}{125}e^{5x}\left(25x^{2}-10x-223\right)

Passez une bonne soirée et allez les bleus !


Rechercher
Menu
Espace membre
18 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1741 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !