Inscription / Connexion Nouveau Sujet
volume d'une sphère intégration et dérivation
bonjour,
voilà ma prof nous a donné un travaux dirigé pour les vacances mais je n'y arrive pas ! 
je suis un peu perdu voila l'énoncé :
(O;OI;OJ:OK) est un repère orthonormal de l'espace.
S est la sphère de centre O et de rayon R (R>0).Pour tout réel z tel que -R<z<R, le plan P parrallèle à (OIJ) de cote z coupe la sphère S suivant le cercle C.
a) Calculer l'aire A(z) du cercle C en fonction de R et z.
b) Le volume V de la sphère S est donné par l'intégrale V= -RRA(z)dz.
-RRA(z)dz.
Démontrer en calculant cette intégrale que V=(4/3) R3
R3
Je bloque déjà à la première question avec l'aire car l'aire du cercle =>  r² mais ici on a pas r et je n'arrive pas à le trouver !
r² mais ici on a pas r et je n'arrive pas à le trouver ! 
merci d'avance
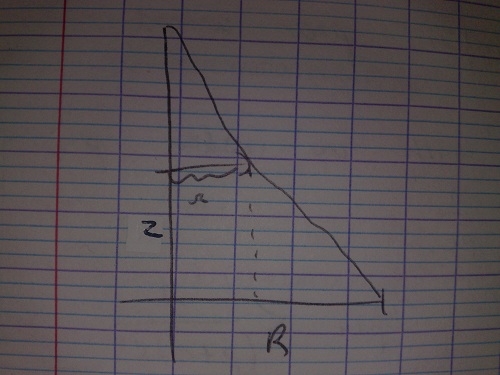
j'ai fait un dessin mais je ne comprends pas comment tu trouve ce résultat regarde l"image je vais te mettre le schéma que j'ai réalisé
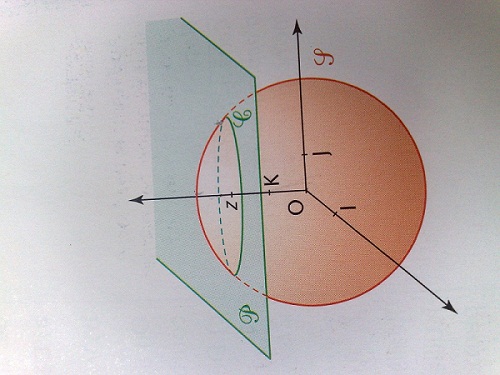
Mais R est le rayon de la sphère : sur ton dessin tu le vois qui va de l'origine à l'extrémité droite de ton petit rayon r, donc R est l'hypothénuse d'un triangle rectangle !
donc A(z)= r²
r²
A(z)= (R²-z²)
(R²-z²)
ainsi j'ai bien calculer l'aire A(z)
pour la deuxième question il suffit de faire l'intégrale de l'aire du cercle ?
donc  -RR
-RR (R²-z²)dz
(R²-z²)dz
et là je peux sortir le  normalement avec les propriétés des intégrales ?
normalement avec les propriétés des intégrales ?

 -RR(R²-z²)dz
-RR(R²-z²)dz
est-ce que j'ai bon jusque là ? 
mais après je sais pas trop quoi faire ... 
Salut,
Tu as bien , mais attention au commentaire : ce n'est pas "l'intégrale de l'aire du cercle"; tu dois voir A(z)dz comme le volume d'une petite tranche de sphère, de section A(z) et d'épaisseur dz; et l'intégrale est la somme de ces volumes !
Maintenant, pour le calcul : une primitive de  (R2-z2) est
(R2-z2) est  (R2z - z3/3).
(R2z - z3/3).
A toi !
bonjour,
désolé je reviens aujourd'hui seulement merci de m'avoir répondu PIL, donc si j'ai bien compris on a :
V=A(z)dz
donc:
V= (R²-z²)dz
(R²-z²)dz
je doit trouver la primitive donc R² est un nombre constant donc on lui rajoute z et z² on obtient z² donne z3
on a donc V=[ (R²z-
(R²z-)]
d'où V= (R3-
(R3-)-(
 (-R3+
(-R3+
et si je calcule je trouve :
V=()
 R3
R3
 merci beaucoup PIL pour ton aide !!
merci beaucoup PIL pour ton aide !! 
bonne journée à tout le monde

 je suis vraiment nul ! ^^ merci
je suis vraiment nul ! ^^ merci



