Inscription / Connexion Nouveau Sujet
Volume maximal
Bonsoir, j'aurais besoin d'aide pour résoudre l'exercice que voici:
1. Joe dispose d'un disque de tissu de rayon 2 mètres.Il souhaite fabriquer un tipi de base circulaire et de volume maximal en utilisant ce tissu. Quel secteur circulaire doit t-il découper dans le tissu?
Aide: Si r est le rayon de la base du tipi, on montrera que le bolume du tipi est
V(r)=(1/3)*
*r²*
(4-r²)
2. Tom fait remarquer a Joe que le problème de son tipi de volume maximal est qu'un homme de taille moyenne ne pourra pas tenir debout dedans. La remarque de Tom est-elle exacte ?
Merci d'avance pour votre aide, car je ne vois pas du tout par où commencer.
Bonjour,
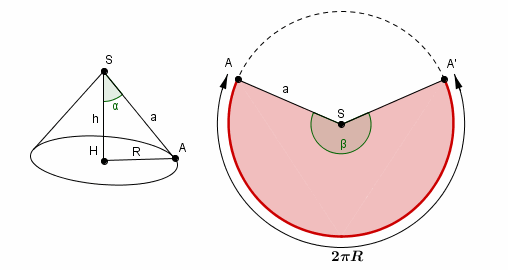
par Pythagore pour écrire la hauteur du cone en fonction de son rayon (R) et de son côté (alias apothème, génératrice) a = 2
Merci mais je ne vois pas très bien comment faire . Si j'ai bien compris il faut montrer que h=(4-r²) or on ne connait ni le rayon, ni a donc je ne vois pas comment appliquer le theoreme de pythagore. parcontre des que j'aurais prouvé que h=(4-r²) , je peux etudier les variations de la fonction avec le signe de la dérivé pour trouver le maximum et ainsi l'aire maximum ?
a c'est 2 m
tu n'as pas bien regardé la figure sans doute et lu l'énoncé :
un disque de tissu de rayon 2 mètres
il vaut donc 2 m ce rayon de la figure de droite
et c'est le "coté" a du cone. le "a" dans ma figure c'est le même à gauche et à droite. et le R aussi d'ailleurs
quant à r (mon R) bien entendu qu'on ne le connait pas !! c'est notre variable
et alors on calcule h en fonction de r etc ...
Bonjour à tous!
Moi, j'ai réussi à trouvé l'aire maximale mais je ne vois absolument pas comment savoir quel secteur circulaire doit être enlevé.
Merci d'avance
Merci, j'ai donc réussi a prouver que h=(4-x²) et j'ai réussi a trouvé R pour que l'aire soit maximale. Cependant je me pose la meme question que lapetitemarmotte, je ne vois pas comment savoir quel secteur circulaire on doit découper.
remarque qu'on demande le volume maximum 
quant à la forme exacte du patron (l'angle 
), une fois qu'on connait r (R sur mon dessin)
une simple proportionnalité donne la valeur de
un cercle complet de rayon a : longueur 2a 360°
un arc d'angle : longueur 2r
(la longueur de l'arc est égale au périmètre de la base du cone, et cette longueur est proportionnelle à l'angle )
Merci beaucoup, et oui j'avais bien calculer le volume maximal, je me suis trompée dans ma reponse.
Je trouve donc que l'angle est 
294° pour R=(8/3).
J'en déduis donc que Joe doit decouper un secteur circulaire de longueur 2*(8/3) et d'angle égal a 293° ?
Oui.
(pourquoi ton 294 se transforme en 293 ??)
en fait cela veut dire qu'il retire un secteur d'angle 360 - 294 = 66° et qu'il garde le reste pour faire son tipi
C'est bien 294, je me suis trompée quand je l'ai réecrit.
Sinon merci, j'ai donc pu terminer l'exercice grace a votre aide
Bonjour,
J'ai le même exercice et je suis bloqué lorsqu'il faut trouver le volume maximal. En effet je trace mon tableau de variation mais voila je trouve que le volume maximal est 2 pour r=0. Je pense mettre trompé quelque part mais je ne sais pas ou.
ce n'est pas une erreur de calcul, c'est une erreur de compréhension !!
on ne te demande pas le tipi qui a une hauteur h maximale !!
on te demande celui qui a un volume maximal
la fonction du volume est d'ailleurs donnée dans l'énoncé :
c'est cette fonction là qu'il faut étudier, dériver etc ... pour en trouver le maximum.
Pour trouver le secteur circulaire il faut si j'ai bien compris trouver r, cependant je ne vois pas comment faire ...
il faut d'abord résoudre les questions dans l'ordre :
Il souhaite fabriquer un tipi de base circulaire et de volume maximal en utilisant ce tissu
c'est à dire qu'il faut déja calculer le volume en fonction de r
(r est une inconnue, et même à cet instant une simple variable)
puis étudier cette fonction volume en fonction de r
et en déduire la valeur de r qui donne ce volume maximal
et alors ... eh bien, on le connait maintenant r !
et donc on peut en déduire ensuite le secteur circulaire
Annuler
connectez vous